题目内容
11.生活中,有人喜欢把传送的便条折成“ ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(图①)长为2 6 厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BE=21厘米;在图③中,BF=19厘米; 在图④中,BM=15厘米.
(2)如果长方形纸条的宽为x厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(结果用x表示).
分析 (1)结合图形、根据旋转的性质计算即可;
(2)根据纸条两端超出点P的长度相等、轴对称图形的概念计算即可.
解答 解:(1)图②中BE=AB-AM-EM=21厘米,
图③中BF=19 厘米,
图④中BM=15厘米,
故答案为:21;19;15;
(2)因为图④为轴对称图形
所以AP=BM=$\frac{26-5x}{2}$,AM=AP+PM=$\frac{26-5x}{2}$+x=13-$\frac{3}{2}$x,
即开始折叠时点M与点A的距离是($13-\frac{3}{2}x$)厘米.
点评 本题考查的旋转变换的性质、轴对称图形的概念,正确根据题意列出代数式是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
3.在平面直角坐标系xOy中,已知点A的坐标为(m,n),其中m>0,n>0,连接OA,将线段OA绕点O按顺时针方向旋转90°得OA1,则点A1的坐标为( )
| A. | (-m,n) | B. | (m,-n) | C. | (n,-m) | D. | (-n,m) |
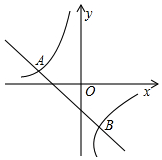 如图,已知一次函数与反比例函数y=$\frac{k}{x}$的图象相交于点 A(-3,1)和点B(a,-3)
如图,已知一次函数与反比例函数y=$\frac{k}{x}$的图象相交于点 A(-3,1)和点B(a,-3)