题目内容
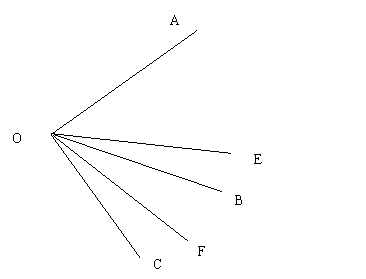
如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是 | AB |
 线分别交PA、PB于点D、E.
线分别交PA、PB于点D、E.(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
分析:(1)可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于PA+PB的结论;
(2)连接AB,根据切线长定理求证PA=PB,再三角形内角和定理求出∠PAB和∠PBA的度数,然后再利用BF为圆直径即可求出∠AFB的度数.
(2)连接AB,根据切线长定理求证PA=PB,再三角形内角和定理求出∠PAB和∠PBA的度数,然后再利用BF为圆直径即可求出∠AFB的度数.
解答:解:(1)∵DA,DC都是圆O的切线,
∴DC=DA,
同理EC=EB,
∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B
∴PA=PB,
∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,
即三角形PDE的周长是8;
(2)连接AB,
∵PA=PB,
∴∠PAB=∠PBA,
∵∠P=40°,
∴∠PAB=∠PBA=
(180-40)=70°,
∵BF⊥PB,BF为圆直径
∴∠ABF=∠PBF=90°-70°=20°
∴∠AFB=90°-20°=70°.
答:(1)若PA=4,△PED的周长为8;
(2)若∠P=40°,∠AFB的度数为70°.
∴DC=DA,
同理EC=EB,
∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B
∴PA=PB,
∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,
即三角形PDE的周长是8;
(2)连接AB,

∵PA=PB,
∴∠PAB=∠PBA,
∵∠P=40°,
∴∠PAB=∠PBA=
| 1 |
| 2 |
∵BF⊥PB,BF为圆直径
∴∠ABF=∠PBF=90°-70°=20°
∴∠AFB=90°-20°=70°.
答:(1)若PA=4,△PED的周长为8;
(2)若∠P=40°,∠AFB的度数为70°.
点评:本题考查的是切线长定理,题图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.

练习册系列答案
相关题目
 25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.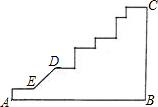 如图所示是某地地形的一部分(除D,E外每个拐角都是直角),从A到C有两条道路,一条是从A经过B再到C,另一条是从A经过E,D等地再到C.如何走近一些呢?
如图所示是某地地形的一部分(除D,E外每个拐角都是直角),从A到C有两条道路,一条是从A经过B再到C,另一条是从A经过E,D等地再到C.如何走近一些呢? 已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.