题目内容
3.计算:(1)$\sqrt{5}$×$\sqrt{3}$
(2)$\sqrt{5}$×$\sqrt{20}$
(3)-3$\sqrt{xyz}$×$\sqrt{\frac{1}{xy}}$
(4)$\sqrt{5ab}$×$\sqrt{\frac{b}{125a}}$(a>0,b>0)
分析 (1)根据二次根式的乘法:$\sqrt{a}$×$\sqrt{b}$=$\sqrt{ab}$,可得答案;
(2)根据二次根式的乘法:$\sqrt{a}$×$\sqrt{b}$=$\sqrt{ab}$,可得答案;
(3)根据系数乘系数,被开方数乘被开方数,可得二次根式的乘法,根据二次根式的乘法:$\sqrt{a}$×$\sqrt{b}$=$\sqrt{ab}$,可得答案;
(4)根据二次根式的乘法:$\sqrt{a}$×$\sqrt{b}$=$\sqrt{ab}$,可得答案.
解答 解:(1)原式=$\sqrt{5×3}$=$\sqrt{15}$;
(2)原式=$\sqrt{5×20}$=$\sqrt{100}$=10;
(3)原式=-3$\sqrt{xyz}$•×$\sqrt{\frac{1}{xy}}$=-3$\sqrt{xyz×\frac{1}{xy}}$=-3$\sqrt{z}$;
(4)原式=$\sqrt{5ab×\frac{b}{125a}}$=$\sqrt{\frac{{b}^{2}}{25}}$=$\frac{b}{5}$.
点评 本题考查了二次根式的乘法,二次根式的运算法则:乘法法则$\sqrt{a}$$•\sqrt{b}$=$\sqrt{ab}$.

练习册系列答案
相关题目
13.$\frac{1}{4}$的倒数是( )
| A. | -$\frac{1}{4}$ | B. | -4 | C. | $\frac{1}{4}$ | D. | 4 |
18.已知三角形三条边的长度是三个连续的自然数,且它的周长小于18,符合上述条件的三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 在一次抽奖活动中,主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后,如果这次抽奖共分三等,其中一等奖1个,二等奖2相,三等奖3个,那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$.
在一次抽奖活动中,主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后,如果这次抽奖共分三等,其中一等奖1个,二等奖2相,三等奖3个,那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$.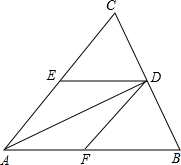 如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.
如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.