题目内容
 如图,矩形OABC,AB∥x轴,点B(9,6),过点B、C的⊙P与y轴相切于点D,且与x轴交于另一点为E.
如图,矩形OABC,AB∥x轴,点B(9,6),过点B、C的⊙P与y轴相切于点D,且与x轴交于另一点为E.(1)求点A、E的坐标;
(2)求过点A、E、C三点的抛物线的解析式.
考点:切线的性质,待定系数法求二次函数解析式
专题:
分析:(1)根据B的坐标即可求得A的坐标,连接DP并延长交BC于F,那么不难得出DF⊥BC,根据垂径定理可知CF=BF=3,由此可求出D点的坐标.求E点坐标,关键是求OE的长,可连接BE、DE、BD,由于∠ECB=90°,因此BE必过圆心P,则∠EDB=90°,因此可通过相似三角形OED和ABD来求出OE的长,即可得出E点的坐标.
(2)根据A、C、E的坐标,用待定系数法即可求出抛物线的解析式.
(2)根据A、C、E的坐标,用待定系数法即可求出抛物线的解析式.
解答: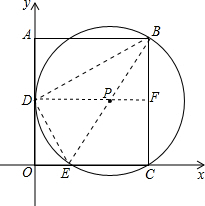 解:(1)连接DP并延长交BC于F,
解:(1)连接DP并延长交BC于F,
∵矩形OABC,AB∥x轴,点B(9,6),
∴A的坐标为(0,6),
由于OA与圆P相切于D,因此DF⊥OA.
∵BC∥OA,
∴DF⊥BC
∴BF=FC=OD=AD=3,
即D点的坐标为(0,3)
连接BE、DE、BD,
∵∠ECB=90°,
∴BE是圆P的直径,
∴∠EDB=90°,
可得△OED∽△ADB,
∴
=
,
OE=
=
=1,
因此E点的坐标为(1,0).
(2)已知A,C,E的坐标分别为(0,6),(9,0),(1,0).
可设过这三点的抛物线的解析式为y=ax2+bx+c,
则有
,
解得
,
因此抛物线的解析式为y=
x2-
x+6.
 解:(1)连接DP并延长交BC于F,
解:(1)连接DP并延长交BC于F,∵矩形OABC,AB∥x轴,点B(9,6),
∴A的坐标为(0,6),
由于OA与圆P相切于D,因此DF⊥OA.
∵BC∥OA,
∴DF⊥BC
∴BF=FC=OD=AD=3,
即D点的坐标为(0,3)
连接BE、DE、BD,
∵∠ECB=90°,
∴BE是圆P的直径,
∴∠EDB=90°,
可得△OED∽△ADB,
∴
| AD |
| OE |
| AB |
| OD |
OE=
| AD•OD |
| AB |
| 3×3 |
| 9 |
因此E点的坐标为(1,0).
(2)已知A,C,E的坐标分别为(0,6),(9,0),(1,0).
可设过这三点的抛物线的解析式为y=ax2+bx+c,
则有
|
解得
|
因此抛物线的解析式为y=
| 2 |
| 3 |
| 20 |
| 3 |
点评:本题主要考查了矩形的性质,切线的性质,圆周角定理,相似三角形的应用以及二次函数解析式的确定等知识点,综合性较强.

练习册系列答案
相关题目
计算2a-3(a-b)的结果是( )
| A、-a+3b | B、a-3b |
| C、a+3b | D、-a-3b |
计算机是将信息转化成二进制进行处理的,二进制即“逢二进一”.将二进制转化成十进制数,例如:(1)2=1×20=1;(10)2=1×21+0×20=2=1;(101)2=1×20+0×21+1×20=5.则将二进制数(1101)2转化成十进制数的结果为( )
| A、8 | B、13 | C、15 | D、16 |
近似数34.2万精确到的数位是( )
| A、十分位 | B、十位 | C、百位 | D、千位 |
 如图,∠ADB=90°,∠BEC=90°,∠ABC=90°.
如图,∠ADB=90°,∠BEC=90°,∠ABC=90°. 将正整数按图所示的规律排列,若用有序数对(m,n)表示第m排从左到右第n个数,如(4,3)表示整数9,则(7,2)表示的整数是
将正整数按图所示的规律排列,若用有序数对(m,n)表示第m排从左到右第n个数,如(4,3)表示整数9,则(7,2)表示的整数是