题目内容
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.

(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″ C″,并求边A′B′在旋转过程中扫过的图形面积.
C″,并求边A′B′在旋转过程中扫过的图形面积.
(1)见解析;(2)5π.
【解析】
试题分析:(1)连接B′O并延长,使O B'=2OB,连接AO并延长,使O A'=2OA,连接CO并延长,使O C'=2OC,连接A'B',A'C',B'C',则△A'B'C'为所求;(2)分别确定出点A'、C'旋转后的对应点A''、C'',连接A''B',B'C'',A''C'',△A''B'C''为所求,利用扇形面积公式可得边A′B′在旋转过程中扫过的图形面积.
试题解析:【解析】
(1)见图中△A'B'C' 3分
(2)见图中△A''B'C'' ..6分
S= π×(22+42)=
π×(22+42)= π×20=5π(平方单位).
π×20=5π(平方单位).
..8分

考点:1.作位似图形;2.图形的旋转;3.扇形面积.

练习册系列答案
相关题目
 的值为零,则x的值为 .
的值为零,则x的值为 . 
 (
( ,
, )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
 ,求反比例函数的解析式.
,求反比例函数的解析式. 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
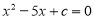 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )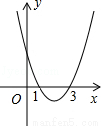

 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗?