题目内容
19.小华每天早上要在七点半以前赶到距家1200米学校上课,一天,小华以0.8米/秒的速度出发,5分钟后,小华的妈妈发现他忘记了带英语书.于是,妈妈立即以1.2米/秒的 速度去追小华,并且在路上追上他.试问:妈妈在距离学校多远的地方追上小华?小华出发多少时间被妈妈追上?分析 设妈妈用x秒追上小华,由题意知小华比妈妈多走5分钟,小华和妈妈走的路程一样,由此等量关系列出方程求解即可.
解答 解:设妈妈用x秒追上小华,那么小华走了(x+5)分钟,
由题意得:0.8(x+5×60)=1.2x,
解得:x=600.
即妈妈用600秒追上小华.
追上小华时,妈妈距离学校有1200-1.2×600=480(米),
小华出发时间为5+600÷60=15(分).
答:妈妈在距离学校480米远的地方追上小华,小华出发15分钟被妈妈追上.
点评 本题考查一元一次方程的应用问题,关键在于弄清题意,找出等量关系即:小华妈妈和小华所行路程相等,列出方程求解.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.若关于x的不等式组$\left\{\begin{array}{l}{3x-2<7}\\{x<a}\end{array}\right.$的解集是x<3,则下列结论正确的是( )
| A. | a=3 | B. | a≤3 | C. | a>3 | D. | a≥3 |
10.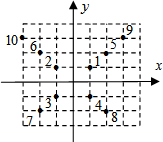 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列各组中,是同类项的是( )
| A. | 2与52 | B. | 2abc与-3ac | C. | -2xy与-2ab | D. | 3x2y与3xy2 |
9.已知m=$({-\frac{{\sqrt{3}}}{3}})×({-\sqrt{21}})$,则有( )
| A. | 2<m<3 | B. | 3<m<4 | C. | -3<m<-2 | D. | -4<m<-3 |
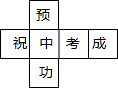
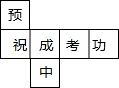
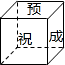 李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )
李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )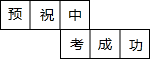
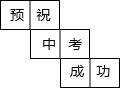
 如图,两条直线a,b相交于O,若∠α=60°,则∠β=120°.
如图,两条直线a,b相交于O,若∠α=60°,则∠β=120°. 如图,在矩形纸片ABCD中,AB=6cm,点E在BC上,且AE=CE,若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=12cm.
如图,在矩形纸片ABCD中,AB=6cm,点E在BC上,且AE=CE,若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=12cm.