题目内容
如图，已知
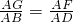，GE∥BC．求证：EF∥CD．
证明：∵GE∥BC，
∴△AGE∽△ABC，
∴
=
，
∵=
，
∴=，
又∵∠CAD=∠EAF，
∴△AEF∽△ACD，
∴∠AFE=∠D，
∴EF∥CD．
分析：先判定出△AGE和△ABC相似，根据相似三角形对应边成比例可得=，从而得到=，再根据两边对应成比例，夹角相等，两三角形相似求出△AEF∽△ACD，根据相似三角形对应角相等得到∠AFE=∠D，然后根据同位角相等，两直线平行证明即可．
点评：本题考查了相似三角形的判定与性质，主要利用了两边对应成比例且夹角相等的两三角形相似，以及相似三角形对应角相等的性质，求出=是证明的关键．
∴△AGE∽△ABC，
∴
=，∵
=，∴
=，又∵∠CAD=∠EAF，
∴△AEF∽△ACD，
∴∠AFE=∠D，
∴EF∥CD．
分析：先判定出△AGE和△ABC相似，根据相似三角形对应边成比例可得
=，从而得到=，再根据两边对应成比例，夹角相等，两三角形相似求出△AEF∽△ACD，根据相似三角形对应角相等得到∠AFE=∠D，然后根据同位角相等，两直线平行证明即可．点评：本题考查了相似三角形的判定与性质，主要利用了两边对应成比例且夹角相等的两三角形相似，以及相似三角形对应角相等的性质，求出
=是证明的关键． 
练习册系列答案
相关题目
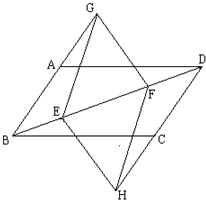19、如图，已知在?ABCD中，E、F是对角线BD上的两点，BE=DF，点G、H分别在BA和DC的延长线上，且AG=CH，连接GE、EH、HF、FG．求证：四边形GEHF是平行四边形．
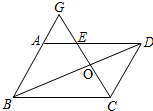如图：已知在平行四边形ABCD中，E是AD上一点，CE与BD相交于点O，CE与BA的延长线相交于点G，已知DE=2AE，CE=10．
如图：已知 点A、E、F、B在一条直线上，AE=BF，CF=DE，AC=BD，
如图，已知在等腰Rt△BCD中，∠BDC=90°，BF平分∠DBC，与CD相交于点F，延长BD到A，使DA=DF，延长BF交AC于E，H是BC边的中点，连接DH与BE相交于点G