题目内容
 如图:已知 点A、E、F、B在一条直线上,AE=BF,CF=DE,AC=BD,
如图:已知 点A、E、F、B在一条直线上,AE=BF,CF=DE,AC=BD,求证:GE=GF.
分析:由条件AE=BF根据等式的性质就可以得出AF=BE,再由SSS就可以得出△ACF≌△BDE,就可以得出∠AFC=∠BED,就可以得出GE=GF.
解答:证明:∵AF=BE,
∴AF+EF=BE+EF,
即AF=BE.
在△ACF和△BDE中,
,
∴△ACF≌△BDE(SSS),
∴∠AFC=∠BED,
∴GE=GF.
∴AF+EF=BE+EF,
即AF=BE.
在△ACF和△BDE中,
|
∴△ACF≌△BDE(SSS),
∴∠AFC=∠BED,
∴GE=GF.
点评:本题考查了等式的性质的运用,全等三角形的判定及性质的运用,等腰三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )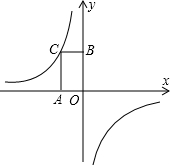 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=