题目内容
4.已知a2+b+4a+6b+13=0,求a2+2b的值.分析 先利用配方法得到(a+2)2+(b+3)2=0,则根据非负数的性质得到a=-2,b=-3,然后利用代入法计算a2+2b的值.
解答 解:∵a2+b+4a+b2+6b+13=0,
∴a2+4a+4+b2+6b+9=0,
∴(a+2)2+(b+3)2=0,
∴a+2=0,b+3=0,解得a=-2,b=-3,
∴a2+2b=(-2)2+2×(-3)=-2.
点评 本题考查了配方法的应用:利用配方法求二次三项式是一个完全平方式时所含字母系数的值.关键是:二次三项式是完全平方式,则常数项是一次项系数一半的平方.也考查了非负数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知点M(x,-1)与N(2,y)关于y轴对称,则xy的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 4 |
15.已知点A(-1,m)和B(1,n)在函数y=$\frac{1}{3}$x+k的图象上,则下列结论中一定正确的是( )
| A. | m>n | B. | m<n | C. | k>0 | D. | k<0 |
11.下列说法中,错误的是( )
| A. | 4的算术平方根是2 | B. | $\sqrt{81}$的平方根是±9 | ||
| C. | 8的平方根是$±2\sqrt{2}$ | D. | 平方根等于1的实数是1 |
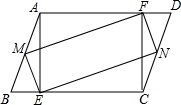 如图,?ABCD中,AE⊥BE于E,CF⊥AD于F,M、N分别为AB、CD的中点.求证:四边形MENF是平行四边形.
如图,?ABCD中,AE⊥BE于E,CF⊥AD于F,M、N分别为AB、CD的中点.求证:四边形MENF是平行四边形.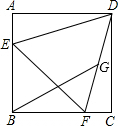 如图,边长为4的正三角形DEF与正方形ABCD共有一顶点D,点E、F分别在线段AB、BC上,将点B与线段DF的中点G连接,则线段BG的长是$\sqrt{6}$+$\sqrt{2}$.
如图,边长为4的正三角形DEF与正方形ABCD共有一顶点D,点E、F分别在线段AB、BC上,将点B与线段DF的中点G连接,则线段BG的长是$\sqrt{6}$+$\sqrt{2}$.