Question

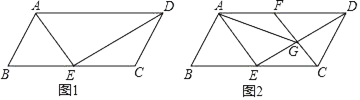
【题目】我们学过角的平分线的概念．类比给出新概念：从一个角的顶点出发，把这个角分成的两个角的射线，叫做这个角的三分线．显然，一个角的三分线有两条，例如：如图1，若，则是的一条三分线．

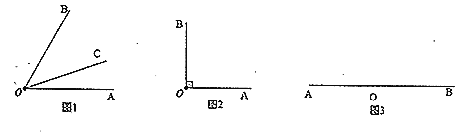
（1）如图1，若，若，求的度数；

（2）如图2，若，若是的两条三分线．

①求的度数；

②现以O为中心，将顺时针旋转度（）得到，当恰好是的三分线时，则求的值．

（3）如图3，若，是的一条三分线，分别是与的平分线，将绕点以每秒的速度沿顺时针方向旋转一周，在旋转的过程中，若射线恰好是的三分线，则此时绕点旋转的时间是多少秒？（直接写出答案即可，不必说明理由）

Answer 1

【答案】（1）；（2）①，②40或50；（3）25，26，28或29秒

【解析】

（1）由OC是∠AOB的一条三分线，且，即可求解；

（2）①由是的两条三分线，可得，即可求解；②以O为中心，将∠COD顺时针旋转n度（n＜360°）得到，当OA恰好是的三分线时，分两种情况：当OA是的三分线，且时；当OA是的三分线，且时，分别求解即可；

（3）由OC是∠AOB的一条三分线，，得或，分两种情况讨论：当时；当时，分别求出∠MON绕点O沿顺时针方向旋转的度数，进而即可求解．

（1）∵OC是∠AOB的一条三分线，且，

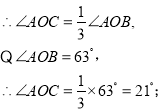
（2）①是的两条三分线，

；

②现以O为中心，将∠COD顺时针旋转n度（n＜360°）得到，当OA恰好是的三分线时，分两种情况：

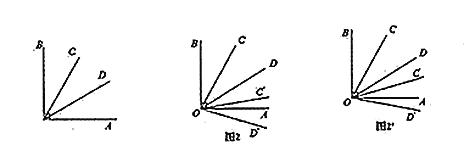
当OA是的三分线，且时，如图2，

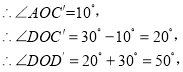
当OA是的三分线，且时，如图2'，

∴n=40或50；

（3）∵OC是∠AOB的一条三分线，，

∴或，

∵OM，ON分别是∠AOC与∠BOC的平分线，

∴，

当时，如图3，

∵60°+180°+20°=260°或60°+180°+40°=280°，

∴∠MON绕点O沿顺时针方向旋转260°或280°时，ON是∠AOC的一条三分线，

∴（秒）或（秒）；

当时，如图3′，

∵30°+180°+40°=250°或30°+180°+80°=290°，

∴绕点沿顺时针方向旋转或时，是的一条三分线，

∴（秒）或（秒）

综上，绕点沿顺时针方向旋转的时间是25，26，28或29秒．