Question

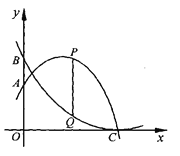
【题目】如图、点A、B分别为抛物线 、与y轴交点，两条抛物线都经过点C（6,0）。点P、Q分别在抛物线 、 上，点P在点Q的上方，PQ平行y轴，设点P的横坐标为m。

（1）求b和c的值

（2）求以A、B、P、Q为顶点的四边形是平行四边形时m的值。

( 3 )当m为何值是，线段PQ的长度取的最大值？并求出这个最大值。

（4）直接写出线段PQ的长度随m增大而减小的m的取值范围。

Answer 1

【答案】（1）， ．（2）m值为或．（3）．（4）≤m＜6.

【解析】整体分析：

（1）把C（6，0）分别代入以这两条抛物线的解析式中，求b，c；（2）分别用含m的代数式表示出点P，Q的纵坐标和PQ的长，用AB=PQ列方程求解；（3）用配方法求PQ的最大值；（4）根据二次函数的性质和x的取值范围求解.

解：（1）∵两条抛物线都经过点C(6，0)，

∴，解得．

，解得．

（2）根据题意，点A的坐标为（0，4），点B的坐标为（0，6），

∴AB2.

∵点P的横坐标为m，

∴P(m, ).

∵PQ平行于y轴，∴Q(m, ).

∴PQ=

．

∴当时， ．

解得,.

∴以A、B、P、Q为顶点的四边形是平行四边形时，

m值为或．

（3）由（2）知，PQ=，

∴当m=时，线段PQ的长度最大，线段PQ的最大长度为．

（4）线段PQ的长度随m的增大而减小的取值范围是≤m＜6