Question

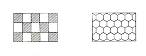
我们常见到如图所示那样图案的地面，它们分别是全用正方形或全用正六边形形状的材料铺成的，这样形状的材料能铺成平整、无空隙的地面．

(1)像上面那样铺地面，能否全用正五边形的材料，为什么？

(2)如果用正方形材料和另一种正n边形材料配合使用，也能像上面那样铺满地面，那么n的值为多少？

(3)如果用正五边形和一种正n边形的材料配合使用，也能像上面那样铺满地面，那么n的值为多少？

Answer 1

答案：
解析：

解　　(1)正五边形的每一个内角都是，如果全用正五边形，要铺满地面必须满足，m×＝，m＝不为整数，所以，不能仅用正五边形一种材料铺满地面． 　　(2)设正n边形的内角为x度，则90＋kx＝360(其中k为正整数)，则kx＝270．由于n＞4，所以180＞x＞90，且x为270的约数．而270＝1×270＝2×135＝3×90＝…，所以 　　x＝135． 　　又由×180＝135可得n＝8． 　　(3)同(2)分析可得n＝10．但实际上，它们不能铺满地面． 　　分析　　用各种正多边形能铺满地面的条件是，各多边形的每一个公共顶点处的所有角之和恰好等于．