Question

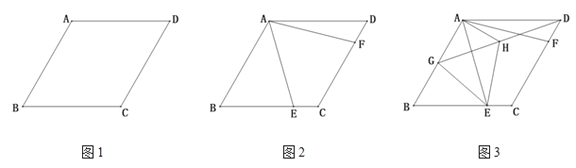
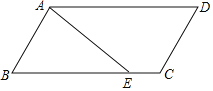
【题目】如图，在平行四边形中，，，，点是折线上的一个动点(不与、重合)．则的面积的最大值是(　　)

A.B.1C.D.

Answer 1

【答案】D

【解析】

分三种情况讨论：①当点E在BC上时，高一定，底边BE最大时面积最大；②当E在CD上时，△ABE的面积不变；③当E在AD上时，E与D重合时，△ABE的面积最大，根据三角形的面积公式可得结论．

解：分三种情况：
①当点E在BC上时，E与C重合时，△ABE的面积最大，如图1，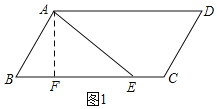

过A作AF⊥BC于F，
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠C+∠B=180°，
∵∠C=120°，
∴∠B=60°，
Rt△ABF中，∠BAF=30°，
∴BF=AB=1，AF=，
∴此时△ABE的最大面积为：×4×=2；
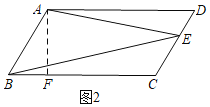
②当E在CD上时，如图2，此时，△ABE的面积=SABCD=×4×=2；

③当E在AD上时，E与D重合时，△ABE的面积最大，此时，△ABE的面积=2，
综上，△ABE的面积的最大值是2；
故选：D．