题目内容
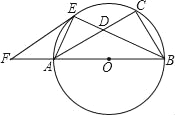
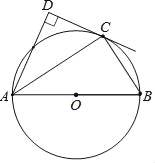
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】分析:(1)连接OC,由![]() 可以得到
可以得到![]() 证出AD∥OC,由平行线的性质证出
证出AD∥OC,由平行线的性质证出![]() ,即可得出结论;
,即可得出结论;
(2)由圆周角定理证出![]() 证明
证明![]() 得出对应边成比例,即可得出结论;
得出对应边成比例,即可得出结论;
(3)由相似三角形的性质得出![]() 得出
得出![]() 求出
求出![]() 在
在![]() 中,由勾股定理即可求出BC的长.
中,由勾股定理即可求出BC的长.
详解:(1)证明:连接OC,如图所示:

∵CD切![]() 于C,
于C,
∴CO⊥CD,
又∵AD⊥CD,
∴AD∥CO.
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
∴AC平分∠BAD.
(2)证明:∵AB为![]() 的直径,
的直径,
∴![]()
∵∠DAC=∠CAO,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴![]()
(3)由(2)得:△ADC∽△ACB,
∴∠ACD=∠B,
∴![]()
∴![]()
∵![]()
∴![]()
在Rt△ABC中,![]()

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】学校为了提高学生跳远科目的成绩,对全校500名九年级学生开展了为期一个月的跳远科目强化训练.王老师为了了解学生的训练情况,强化训练前,随机抽取了该年级部分学生进行跳远测试,经过一个月的强化训练后,再次测得这部分学生的成绩,将两次测得的成绩制作成如图所示的统计图和不完整的统计表
训练后学生成绩统计表
成绩/分数 | 6分 | 7分 | 8分 | 9分 | 10分 |
人数/人 | 1 | 3 | 8 | 5 | n |
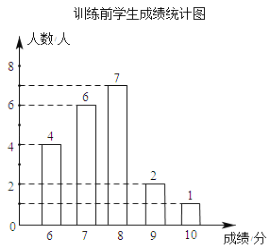
根据以上信息回答下列问题
(1)训练后学生成绩统计表中n= ,并补充完成下表:
平均分 | 中位数 | 众数 | |
训练前 | 7.5 | 8 | |
训练后 | 8 |
(2)若跳远成绩9分及以上为优秀,估计该校九年级学生训练后比训练前达到优秀的人数增加了多少?