题目内容
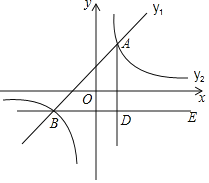
【题目】如图,在![]() 中,
中,![]() ,以点O为圆心的
,以点O为圆心的![]() 经过AB的中点C,连接OC,直线AO与
经过AB的中点C,连接OC,直线AO与![]() 相交于点E,D,OB交
相交于点E,D,OB交![]() 于点F,P是
于点F,P是![]() 的中点,连接CE,CF,BP.
的中点,连接CE,CF,BP.
![]() 求证:AB是
求证:AB是![]() 的切线;
的切线;
![]() 若
若![]() ,则
,则
![]() 当
当![]() ______时,四边形OECF是菱形;
______时,四边形OECF是菱形;
![]() 当
当![]() ______时,四边形OCBP是正方形
______时,四边形OCBP是正方形

【答案】(1)证明见解析(2)①当![]() 时,四边形OECF是菱形②当
时,四边形OECF是菱形②当![]() 时,四边形OCBP是正方形
时,四边形OCBP是正方形
【解析】
(1)利用等腰三角形的性质得![]() ,然后根据切线的判定定理得到结论;
,然后根据切线的判定定理得到结论;
(2)①根据菱形的判定方法,当![]() 时,四边形OECF为菱形,则可判断
时,四边形OECF为菱形,则可判断![]() 为等边三角形,所以
为等边三角形,所以![]() ,然后根据含30°的直角三角形三边的关系可计算出此时AC的长;
,然后根据含30°的直角三角形三边的关系可计算出此时AC的长;
②利用正方形的判定方法,当![]() ,
,![]() 时,四边形OCBP为正方形,则根据正方形的性质计算出此时BC的长,从而得到AC的长.
时,四边形OCBP为正方形,则根据正方形的性质计算出此时BC的长,从而得到AC的长.
(1)证明:![]() ,点C为AB的中点,
,点C为AB的中点,
![]() ,
,
![]() 是
是![]() 的切线;
的切线;
(2)①当![]() 时,四边形OECF为菱形,
时,四边形OECF为菱形,
此时![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,
即当![]() 时,四边形OECF是菱形;
时,四边形OECF是菱形;
②当![]() ,
,![]() 时,四边形OCBP为正方形,
时,四边形OCBP为正方形,
此时![]() ,
,
即当![]() 时,四边形OCBP是正方形.
时,四边形OCBP是正方形.
故答案为![]() ,
,![]() .
.

练习册系列答案
相关题目