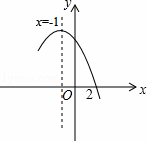��Ŀ����
��ƽ��ֱ������ϵ��, ������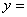
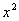 +
+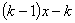 ��ֱ��
��ֱ��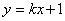 ����A, B���㣬��A�ڵ�B�����.
����A, B���㣬��A�ڵ�B�����.
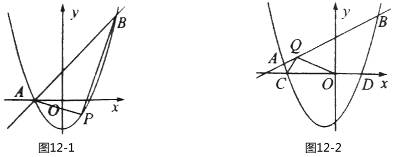
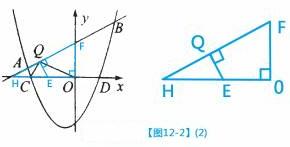
(1) ��ͼ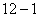 ����
���� ʱ��ֱ��д��A��B��������ꣻ
ʱ��ֱ��д��A��B��������ꣻ
(2) ��(1)�������£���PΪ�������ϵ�һ�����㣬����ֱ��AB�·����������ABP��������ֵ����ʱ��P�����ꣻ
(3) ��ͼ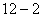 ��������
��������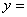
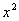 +
+ 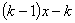
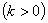 ��
�� �ύ��C��D���㣨��C�ڵ�D����ࣩ.��ֱ��
�ύ��C��D���㣨��C�ڵ�D����ࣩ.��ֱ��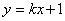 ���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣿�����ڣ��������ʱ
���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣿�����ڣ��������ʱ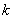 ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.


��1��A(-1,0) ��B(2,3)
���������д����k=1ʱ����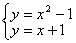 ����ɵ�
����ɵ�
��2��ƽ��ֱ��AB�õ�ֱ��L����L��������ֻ��һ������ʱ����ABP��������ͼ12-1��1����
��ֱ��L����ʽΪ��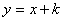 ��
��
����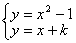 ����
����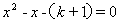
�б�ʽ��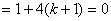 ����ã�
����ã�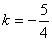
����ԭ�����У��� ����ã�
����ã�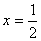 ��
�� 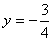
��P��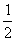 ,
,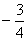 ��
��
����AB��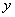 ����M��0��1����ֱ��L����
����M��0��1����ֱ��L����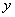 ��G��0��
��G��0��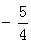 ��
��
��M��MN��ֱ��L��N����OM=1��OA=1�����AMO=45��
�ߡ�AMN=90�����NMO=45��
��RT��MNE�У���NMO=45�㣬MG=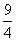 ������ͼ12-1��2����
������ͼ12-1��2����
�� MN= ��MN��Ϊ��ABP�ĸ�
��MN��Ϊ��ABP�ĸ�
���������빫ʽ����ã�AB=
�ʡ�ABP������

��3������ֱ��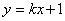 �ϴ���Ψһһ��Qʹ�á�OQC=90��
�ϴ���Ψһһ��Qʹ�á�OQC=90��
���QΪ��OC���е�EΪԲ�ģ�OCΪֱ���γɵ�ԲE��ֱ��
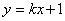 ����ʱ���е㡾��ͼ12-2��1����
����ʱ���е㡾��ͼ12-2��1����
�ɽ���ʽ��֪��C��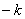 ,0����OC=
,0����OC=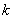 ����ԲE�İ뾶��OE=CE=
����ԲE�İ뾶��OE=CE=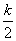 =QE
=QE
��ֱ��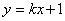 ��
�� ��
��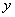 �ύ��H���F�㣬�룬
�ύ��H���F�㣬�룬
 ��F��0,1������OF=1 ��H��
��F��0,1������OF=1 ��H��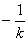 ,0���� ��OH =
,0���� ��OH =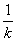
�� EH=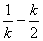
��AB���� ��EQ��AB����EQH=90��
�ڡ�FOH�͡�EQH�� 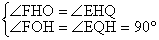
���FOH�ס�EQH
�� �� 1��
�� 1��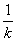 =
=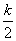 ��QH����QH =
��QH����QH =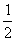
��RT��EQH��EH=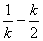 ��QH =
��QH =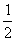 ��QE =
��QE =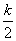 �����ݹ��ɶ����ã�
�����ݹ��ɶ����ã�
 +
+ =
=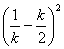
���



 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д� ��
�� ���㷽����
���㷽���� ����
���� ��ֵΪ
��ֵΪ


 ��
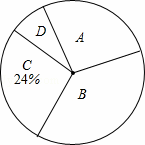
�� ����1=120�㣬���
����1=120�㣬��� �Ķ����� ��.
�Ķ����� ��.
 B
B ��
�� B
B ��3
��3 +
+
 ��
�� =
=

 ��y2���������������㣬��y1��y2��
��y2���������������㣬��y1��y2��