题目内容
两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.

(1)当旋转到顶点D、H重合时,连接AE、CG,求证:△AED≌△GCD(如图②).
(2)当α=45°时(如图③),求证:四边形MHND为正方形.


证明:(1)如图②,∵由题意知,AD=GD,ED=CD,∠ADC=∠GDE=90°,
∴∠ADC+∠CDE=∠GDE+∠CDE,即∠ADE=∠GDC,
在△AED与△GCD中,
 ,
,
∴△AED≌△GCD(SAS);
(2)如图③,∵α=45°,BC∥EH,
∴∠NCE=∠NEC=45°,CN=NE,
∴∠CNE=90°,
∴∠DNH=90°,
∵∠D=∠H=90°,
∴四边形MHND是矩形,
∵CN=NE,
∴DN=NH,

 ∴矩形MHND是正方形.
∴矩形MHND是正方形.

练习册系列答案
相关题目
参加广安市2014年高中阶段教育学生招生考试的学生大约有4.3万人,将4.3万人用科学记数法表示应为( )
|
| A. | 4.3×104人 | B. | 43×105人 | C. | 0.43×105人 | D. | 4.3×105人 |


 的直线与
的直线与 轴平行,且直线分别与反比例函数
轴平行,且直线分别与反比例函数  和
和 的图象交于点
的图象交于点 、点
、点 .
. 的面积为8 ,求k的值 .
的面积为8 ,求k的值 . 


 cm
cm =
= =3,
=3, =
= =10,
=10, =
= =15,…观察以上计算过程,寻找规律计算
=15,…观察以上计算过程,寻找规律计算 =
=  下列图形中,是轴对称图形的是 ( )
下列图形中,是轴对称图形的是 ( )
 (C) (D)
(C) (D)
 千克,付款金额
千克,付款金额 为元,则
为元,则
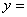
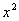 +
+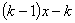 与直线
与直线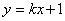 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.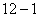 ,当
,当 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;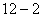 ,抛物线
,抛物线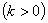 与
与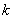 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.