题目内容
将20个数平均分成两组,第一组的平均数为50,方差为33,第二组的平均数为40,方差为45,求这20个数的方差.
考点:方差
专题:计算题
分析:先计算20个数的平均数为45,设第一组数为x1,x2,…,x10,第二组数为x11,x12,…,x20,再利用方差公式得到33=
[x12+x22+…+x102-10×502],45=
[x112+x122+…+x202-10×402],所以x12+x22+…+x102=25330,x112+x122+…+x202=16450,然后再次利用方差公式计算20个数的方差即可.
| 1 |
| 10 |
| 1 |
| 10 |
解答:解:20个数的平均数=
=45,
设第一组数为x1,x2,…,x10,第二组数为x11,x12,…,x20,
根据题意得33=
[x12+x22+…+x102-10×502],45=
[x112+x122+…+x202-10×402],
所以x12+x22+…+x102=25330,x112+x122+…+x202=16450,
所以这20个数的方差S2=
[x12+x22+…+x102+x112+x122+…+x202-20×452]
=
(25330+16450-40500)
=64.
| 50×10+40×10 |
| 20 |
设第一组数为x1,x2,…,x10,第二组数为x11,x12,…,x20,
根据题意得33=
| 1 |
| 10 |
| 1 |
| 10 |
所以x12+x22+…+x102=25330,x112+x122+…+x202=16450,
所以这20个数的方差S2=
| 1 |
| 20 |
=
| 1 |
| 20 |
=64.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[x12+x22+…+xn2-n
2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
| A、2,2,3 |
| B、2,3,4 |
| C、3,4,5 |
| D、5,8,13 |
下列变形正确的是( )
| A、若x2=y2,则x=y | ||||
B、若
| ||||
| C、若x(x-2)=3(x-2),则x=3 | ||||
| D、若(m+n)x=(m+n)y,则x=y, |
 已知直线l和l上一点P,用尺规作l的垂线,使它经过点P.你能明白小明的作法吗?你是怎样作的?
已知直线l和l上一点P,用尺规作l的垂线,使它经过点P.你能明白小明的作法吗?你是怎样作的?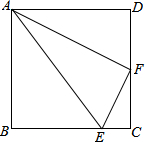 设点E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,BE=3EC,F为CD的中点,连结AF,AE,EF.问△AEF是什么形状的三角形?请说明理由.
设点E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,BE=3EC,F为CD的中点,连结AF,AE,EF.问△AEF是什么形状的三角形?请说明理由.