题目内容
 如图所示的平面直角坐标系中,三角形ABC的顶点坐标分别是A(1,1),B(6,1),C(5,5)
如图所示的平面直角坐标系中,三角形ABC的顶点坐标分别是A(1,1),B(6,1),C(5,5)(1)求三角形ABC的面积;
(2)如果将三角形ABC向右平移3个单位长度,再向上平移2个单位长度,得到三角形A′B′C′,画出平移后的图形,写出点A′B′C′的坐标;
(3)三角形A′B′C′与三角形ABC的大小,形状有什么关系;
(4)将三角形A′B′C′经过怎样的平移可得到三角形ABC?写出一种平移方案.
考点:作图-平移变换
专题:
分析:(1)直接根据三角形的面积公式即可得出结论;
(2)根据图形平移的性质画出图形,写出各点坐标即可;
(3)根据图形平移的性质即可得出结论;
(4)根据两图形的位置即可得出结论.
(2)根据图形平移的性质画出图形,写出各点坐标即可;
(3)根据图形平移的性质即可得出结论;
(4)根据两图形的位置即可得出结论.
解答: 解:(1)S△ABC=
解:(1)S△ABC=
×5×4=10;
(2)如图所示:A′(4,3),B′(9,3),C′(8,7);
(3)由图可知,△A′B′C′与△ABC的大小,形状完全相同;
(4)△A′B′C′先向左平移3个单位,再向下平移两个单位即可得到△ABC.
 解:(1)S△ABC=
解:(1)S△ABC=| 1 |
| 2 |
(2)如图所示:A′(4,3),B′(9,3),C′(8,7);
(3)由图可知,△A′B′C′与△ABC的大小,形状完全相同;
(4)△A′B′C′先向左平移3个单位,再向下平移两个单位即可得到△ABC.
点评:本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
下列方程中是二元一次方程的是( )
| A、xy=9 | ||
| B、3x+2y=19 | ||
| C、x-2y=z | ||
D、
|
化简(-x)-3•(-x)2的值是( )
| A、-x | ||
| B、x | ||
C、-
| ||
D、
|
 已知,如图,∠DCF=100°,∠BEF=100°,试判断直线AB与CD的关系,并说明理由.
已知,如图,∠DCF=100°,∠BEF=100°,试判断直线AB与CD的关系,并说明理由.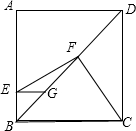 如图,在正方形ABCD中,点E、G分别在边AB、对角线BD上,EG∥AD,F为GD的中点,连接FC,利用勾股定理的逆定理,证明EF⊥FC.
如图,在正方形ABCD中,点E、G分别在边AB、对角线BD上,EG∥AD,F为GD的中点,连接FC,利用勾股定理的逆定理,证明EF⊥FC.