题目内容
如图,点A为双曲线y=
 (x>0)的图象上一点,AB∥x轴交直线y=﹣x于点B.
(x>0)的图象上一点,AB∥x轴交直线y=﹣x于点B.
(1)若点B的纵坐标为2,比较线段AB和OB的大小关系;
(2)当点A在双曲线图象上运动时,代数式“AB2﹣OA2”的值会发生变化吗?请你作出判断,并说明理由.
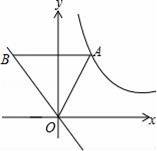

【考点】反比例函数图象上点的坐标特征.
【分析】(1)根据题意求得A、B点的坐标,即可求得AB和OB的长,即可比较线段AB和OB的大小关系;
(2)设A(a,b),则B(﹣b,b),ab=2.所以利用两点间的距离公式可以求得线段AB、OA的长度;然后可以AB2﹣OA2的值.
【解答】解:(1)∵点B的纵坐标为2,AB∥x轴,
∴A(1,2),B(﹣2,2),
∴AB=3,OB=2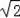
 ,
,
∴AB>OB;
(2)∵直线AB平行于x轴交直线y=
 于点A,
于点A,
故设A(a,b),
∵A为双曲线y=
 (x>0)上一点,
(x>0)上一点,
∴ab=2,
∵B纵坐标为b,
∴B(﹣b,b)
∴AB2﹣OA2=(a+b)2﹣[a2+b2]=2ab=4.
【点评】本题考查了反比例函数与一次函数图象上点的坐标特征,勾股定理的应用,利用点A的横坐标表示出点B的坐标是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目


 ,一个动点P从O出发沿线段OA→线段AB→
,一个动点P从O出发沿线段OA→线段AB→

 B.
B.






 中,以
中,以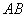 为斜边,作直角
为斜边,作直角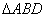 ,使点
,使点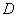 落在
落在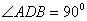 .
.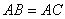 ,
,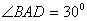 ,
,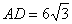 ,点
,点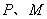 分别为
分别为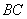 、
、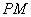 ,求线段
,求线段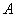 逆时针旋转一定角度,得到
逆时针旋转一定角度,得到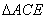 ,连接
,连接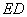 并延长交
并延长交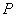 ,求证:
,求证: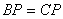 ;
;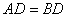 ,过点
,过点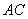 于点
于点 ,交
,交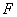 ,
,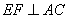 ,且
,且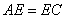 ,请直接写出线段
,请直接写出线段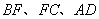 之间的关系(不需要证明).
之间的关系(不需要证明).
 B.2 C.-
B.2 C.-