题目内容
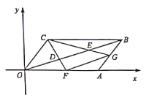
【题目】如图,矩形![]() 中,
中,![]() ,连接
,连接![]() ,以对角线
,以对角线![]() 为边按逆时针方向作矩形
为边按逆时针方向作矩形![]() ,使矩形
,使矩形![]() 矩形
矩形![]() ;再连接
;再连接![]() ,以对角线
,以对角线![]() 为边,按逆时针方向作矩形,使矩形
为边,按逆时针方向作矩形,使矩形![]() 矩形
矩形![]() , ..按照此规律作下去,若矩形
, ..按照此规律作下去,若矩形![]() 的面积记作
的面积记作![]() ,矩形
,矩形![]() 的面积记作
的面积记作![]() ,矩形
,矩形![]() 的面积记作
的面积记作![]() , ... 则
, ... 则![]() 的值为__________.
的值为__________.

【答案】![]()
【解析】
首先根据矩形的性质,求出AC,根据边长比求出面积比,依次类推,得出规律,即可得解.
∵四边形ABCD是矩形,
∴AD⊥DC,
∴AC=![]() ,
,
∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,
∴矩形AB1C1C的边长和矩形ABCD的边长的比为![]() :2
:2
∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,
∵矩形ABCD的面积=2×1=2,
∴矩形AB1C1C的面积=![]() ,
,
依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4
∴矩形AB2C2C1的面积=![]()
∴矩形AB3C3C2的面积=![]() ,
,
按此规律第n个矩形的面积为:![]()
则![]()
故答案为:![]() .
.

练习册系列答案
相关题目