题目内容
15. 小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
分析 根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB-PB求出即可.
解答 解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°,
在△CPD和△PAB中
∵$\left\{\begin{array}{l}{∠CDP=∠ABP}\\{DC=PB}\\{∠DCP=∠APB}\end{array}\right.$,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=36,PB=10,
∴AB=36-10=26(m),
答:楼高AB是26米.
点评 此题主要考查了全等三角形的应用,根据题意得出△CPD≌△PAB是解题关键.

练习册系列答案
相关题目
5.不等式-3x+6>0的正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对某班45名同学视力情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对绥江水质量情况的调查 | |
| D. | 对某类烟花爆竹燃放安全情况的调查 |
10.下面四个图形中∠1与∠2是对顶角的是( )
| A. | 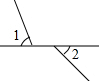 | B. | 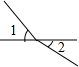 | C. | 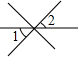 | D. | 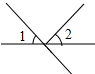 |
20.如表是某校八年级(8)班共50位同学身高情况的频数分布表,则表中的组距是7,身高最大值与最小值的差至多是27cm.
| 组别(cm) | 145.5~152.5 | 152.5~159.5 | 159.5~166.5 | 166.5~173.5 |
| 频数(人) | 9 | 19 | 14 | 8 |
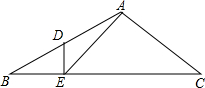 已知:如图,△ABC中,∠B=30°,点D为AB的中点,过点D作DE⊥BC于点E,连结AE,求cos∠AEC的值.
已知:如图,△ABC中,∠B=30°,点D为AB的中点,过点D作DE⊥BC于点E,连结AE,求cos∠AEC的值.