Question

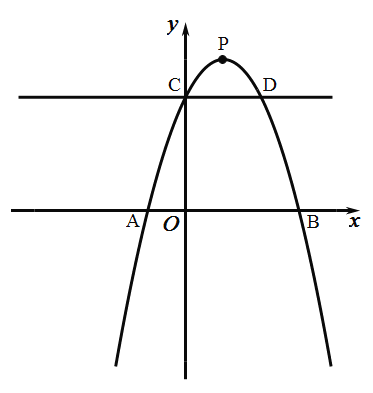
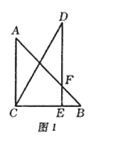
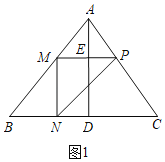
【题目】如图，在△ABC中，BC＝10，高AD＝8，M、N、P分别在边AB、BC、AC上移动，但不与A、B、C重合，连接MN、NP、MP，且MP始终与BC保持平行，AD与MP相交于点E，设MP＝x，△MNP的面积用y表示．

（1）求y关于x的函数关系式；

（2）当x取什么值时，y有最大值，并求出的最大值；

（3）当x取什么值时，△MNP是等腰直角三角形？

Answer 1

【答案】（1）y＝﹣;（0＜x＜10）；（2）x＝5，y最大值是10；（3）或．

【解析】

（1）先证明△AMP∽△ABC求得ED＝8﹣x，再由三角形面积公式即可求得y与x之间的关系；

（2）进行配方求解即可；

（3）分三种情况：∠NMP＝90°，∠MPN＝90°，∠MNP＝90°时，MN＝MP分别求解即可.

（1）∵MP∥BC，AD⊥BC，

∴△AMP∽△ABC，

∴，

∵BC＝10，高AD＝8，MP＝x，

∴，

8x＝10（8﹣ED），

ED＝8﹣x，

∴y＝＝＝﹣（0＜x＜10）；

（2）y＝﹣＝﹣（x﹣5）2+10，

∵﹣＜0，

∴当x＝5时，y有最大值是10；

（3）分三种情况：

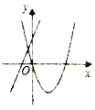
①当∠NMP＝90°，MN＝MP时，如图1，△MNP是等腰直角三角形，

由（1）知：MN＝8﹣x，

∴x＝8﹣x，

x＝；

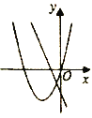
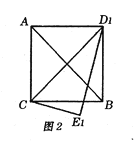
②当∠MPN＝90°，MP＝PN时，如图2，△MNP是等腰直角三角形，

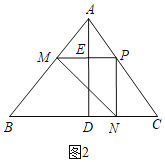
同理得：x＝；

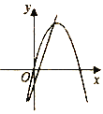
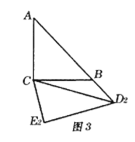
③当∠MNP＝90°，MN＝PN时，如图3，△MNP是等腰直角三角形，

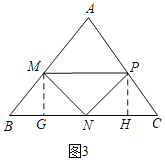
过M作MG⊥BC于G，过P作PH⊥BC于H，

∵MP∥BC，

∴MG＝PH，

∵MN＝NP，

∴Rt△MGN≌Rt△PHN（HL），

∴GN＝NH，

∵MP∥BC，

∴∠MNG＝∠NMP＝45°＝∠HNP＝∠NPM，

∴GM＝GN＝NH＝PH，

由（1）知：MG＝8﹣x，

∵MP＝GN+NH＝2GN，

∴x＝2（8﹣x），

x＝，

综上，当x取或时，△MNP是等腰直角三角形．