题目内容
4.下列各三角形的边长如图所示,其中三角形面积是无理数的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据三角形的面积公式分别计算出各三角形的面积,再根据无理数的定义即可得出结论.
解答  解:A、S=$\frac{1}{2}$×8×3=12,12是有理数,故本选项错误;
解:A、S=$\frac{1}{2}$×8×3=12,12是有理数,故本选项错误;
B、∵($\sqrt{3}$)2+($\sqrt{12}$)2=($\sqrt{15}$)2,∴此三角形是直角三角形,
∴S=$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{12}$=3,3是有理数,故本选项错误;
C、S=$\frac{1}{2}$×5×5×sin60°=$\frac{25\sqrt{3}}{4}$,$\frac{25\sqrt{3}}{4}$是无理数,故本选项正确;
D、S=$\frac{1}{2}$×2×3=3,3是有理数,故本选项错误.
故选C.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
16.下列各式计算正确的是( )
| A. | (x3)3=x6 | B. | -2x-3=-$\frac{1}{2{x}^{3}}$ | C. | 3m2•2m4=6m8 | D. | a6÷a2=a4(a≠0) |
14.P(2,-3)关于x轴的对称的点在第( )象限.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
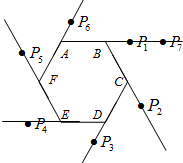 将正六边形ABCDEF的各边按如图所示延长,从射线AB开始分别在各射线上标记点P1、P2、P3、…,按此规律,点P2013在射线CD上.
将正六边形ABCDEF的各边按如图所示延长,从射线AB开始分别在各射线上标记点P1、P2、P3、…,按此规律,点P2013在射线CD上.