Question

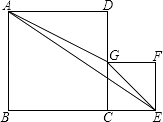
【题目】如图，在△ABC中，AB=AC，∠A=40°，D、E分别是AB、AC上的不动点，且BD+CE=BC,点P是BC上一动点，

（1）当PC=CE时，试求∠DPE的度数

（2）当PC=BD时，∠DPE的度数还会与（1）的结果相同吗？若相同请写出求解过程，若不相同，请说明理由

Answer 1

【答案】（1）70°；（2）相同，理由详见解析

【解析】

（1）根据AB=AC，∠A=40°，可求得∠B和∠C，因为BD+CE=BC，PC=CE，可推得BD=BP，即可求得∠BPD和∠CPE度数，可得出∠DPE度数．

（2）若PC=BD，已知BD+CE=BC，可得BP=CE，证明△BDP和△CPE全等，推出∠BDP=∠CPE，∠DPC=∠DPE+∠CPE=∠B＋∠BDP，即可求出∠DPE度数．

（1）∵AB=AC，∠A=40°

∴∠B=∠C=(180°-40°)÷2=70°

∵BD+CE=BC，PC=CE

∴BD=BP

∴∠BPD=∠CPE=55°

∴∠DPE=180°-55°×2=70°．

故答案为： 70°

（2）相同，PC=BD时，BD+CE=BC，则BP=CE

在△BDP和△CPE中

△BDP≌△CPE（SAS）

∠BDP=∠CPE，∠DPC=∠DPE+∠CPE=∠B＋∠BDP

∴∠DPE=70°

故答案为：相同，理由见解析