题目内容
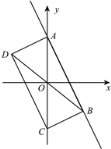
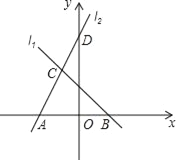
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
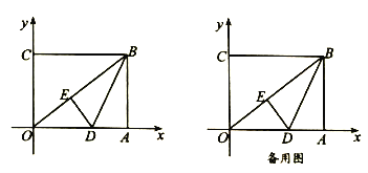
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题。
解:(1)在Rt△ABC中,∵OA=12,AB=9,
![]()
故答案为15.
(2)如图,
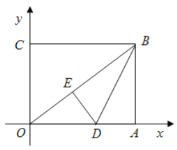
设![]() ,则
,则![]()
根据轴对称的性质,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]()
则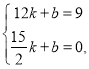 ,
,
解得![]()
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() .
.
故答案为:![]()
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形,再过点
是平行四边形,再过点![]() 作
作![]() 于点
于点![]() ,
,
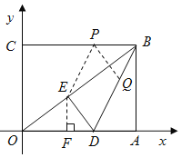
由![]()
得![]() ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
![]()
由于![]() ,所以可设直线
,所以可设直线![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() ,解得
,解得![]()
∴直线![]() 为
为![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]()

练习册系列答案
相关题目