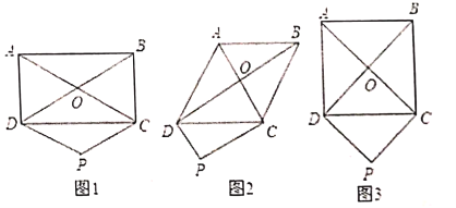
ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌМЧ
жаЃЌМЧ![]() гы
гы![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЃЈ
ЃЈ![]() Ёй0ЃЌnЁй0ЃЉЕФЭМЯѓЮЊЭМаЮG, вбжЊЭМаЮGгы
Ёй0ЃЌnЁй0ЃЉЕФЭМЯѓЮЊЭМаЮG, вбжЊЭМаЮGгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() газюаЁЃЈЛђзюДѓЃЉжЕn, ЕуBЕФзјБъЮЊ(
газюаЁЃЈЛђзюДѓЃЉжЕn, ЕуBЕФзјБъЮЊ(![]() ,
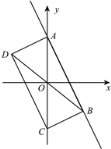
, ![]() )ЃЌЕуAЁЂBЙигкдЕуOЕФЖдГЦЕуЗжБ№ЮЊCЁЂDЃЌШєAЁЂBЁЂCЁЂDжаШЮКЮШ§ЕуЖМВЛдквЛжБЯпЩЯЃЌЧвЖдНЧЯпACЃЌBDЕФНЛЕугыдЕуOжиКЯЃЌдђГЦЫФБпаЮABCDЮЊЭМаЮGЕФАщЫцЫФБпаЮЃЌжБЯпABЮЊЭМаЮGЕФАщЫцжБЯп.
)ЃЌЕуAЁЂBЙигкдЕуOЕФЖдГЦЕуЗжБ№ЮЊCЁЂDЃЌШєAЁЂBЁЂCЁЂDжаШЮКЮШ§ЕуЖМВЛдквЛжБЯпЩЯЃЌЧвЖдНЧЯпACЃЌBDЕФНЛЕугыдЕуOжиКЯЃЌдђГЦЫФБпаЮABCDЮЊЭМаЮGЕФАщЫцЫФБпаЮЃЌжБЯпABЮЊЭМаЮGЕФАщЫцжБЯп.

ЃЈ1ЃЉШчЭМЃЌШєКЏЪ§![]() ЕФЭМЯѓМЧЮЊЭМаЮGЃЌЧѓЭМаЮGЕФАщЫцжБЯпЕФБэДяЪНЃЛ
ЕФЭМЯѓМЧЮЊЭМаЮGЃЌЧѓЭМаЮGЕФАщЫцжБЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌШєЭМаЮGЕФАщЫцжБЯпЕФБэДяЪНЪЧ![]() ЃЌЧвАщЫцЫФБпаЮЕФУцЛ§ЮЊ12ЃЌЧѓ
ЃЌЧвАщЫцЫФБпаЮЕФУцЛ§ЮЊ12ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЃЈmЃО0ЃЌn ЃМ0ЃЉЕФБэДяЪНЃЛ
ЃЈmЃО0ЃЌn ЃМ0ЃЉЕФБэДяЪНЃЛ
ЃЈ3ЃЉШчЭМЃЌШєЭМаЮGЕФАщЫцжБЯпЪЧ![]() ЃЌЧвАщЫцЫФБпаЮABCDЪЧОиаЮЃЌЧѓЕуBЕФзјБъ.
ЃЌЧвАщЫцЫФБпаЮABCDЪЧОиаЮЃЌЧѓЕуBЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУХзЮяЯпНтЮіЪНШЗЖЈAЕуКЭBЕузјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓАщЫцжБЯпЕФНтЮіЪНЃЛ
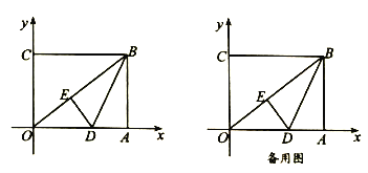
ЃЈ2ЃЉШчЭМ2ЃЌзїBEЁЭACгкЕуEЃЌРћгУвЛДЮКЏЪ§НтЮіЪНКЭЙигкдЕуЖдГЦЕФзјБъЬиеїЕУЕНAЃЈ0ЃЌ-3ЃЉКЭCЃЈ0ЃЌ3ЃЉЃЌдйРћгУЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ12ПЩЧѓГіBE=2ЃЌдђBЕуЕФКсзјБъЮЊ2ЃЌдђРћгУЖЅЕуBдкжБЯп![]() ЩЯЕУЕНЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ-1ЃЉЃЌдђЩшЖЅЕуЪНy=aЃЈx-2ЃЉ2-1ЃЌШЛКѓАбAЕузјБъДњШыЧѓГіaМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЛ
ЩЯЕУЕНЖЅЕуBЕФзјБъЮЊЃЈ2ЃЌ-1ЃЉЃЌдђЩшЖЅЕуЪНy=aЃЈx-2ЃЉ2-1ЃЌШЛКѓАбAЕузјБъДњШыЧѓГіaМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЛ
ЃЈ3ЃЉШчЭМЃЌзї![]() жсгкЕу
жсгкЕу![]() ,гЩ
,гЩ![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌПЩЕУЕуBЕФзјБъЮЊЃЈ
ЩЯЃЌПЩЕУЕуBЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдкRtЁїOEBжаЃЌгЩЙДЙЩЖЈРэЧѓГіmЕФжЕЃЌДгЖјПЩЧѓГіЕуBЕФзјБъ.
ЃЉЃЌдкRtЁїOEBжаЃЌгЩЙДЙЩЖЈРэЧѓГіmЕФжЕЃЌДгЖјПЩЧѓГіЕуBЕФзјБъ.
ЃЈ1ЃЉгЩЬтвтЕУ![]()
![]() ЃЌ
ЃЌ
ЩшЫљЧѓАщЫцжБЯпЕФБэДяЪНЮЊ![]() ЃЌ
ЃЌ
дђ![]()
НтЃЌЕУ![]()
ЫљвдКЏЪ§y=ЃЈx-2ЃЉ2+1ЕФАщЫцжБЯпЕФБэДяЪНЪЧ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЃЌзїBEЁЭACгкЕуE,
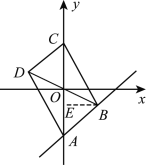
гЩЬтвтжЊЃЌ
OC=OAЃЌOB=ODЃЌ
ЁрЫФБпаЮABCDЪЧЦНааЫФБпаЮ.
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ12ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ,
,
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃО0ЃЌМДЖЅЕуBдк
ЃО0ЃЌМДЖЅЕуBдк![]() жсЕФгвВрЃЌЧвдкжБЯп
жсЕФгвВрЃЌЧвдкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЭМаЮGОЙ§Еу![]() ,
,
ЩшЖЅЕуЪНy=aЃЈx-2ЃЉ2-1ЃЌ
Ёр4a=-2ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЌзї![]() жсгкЕу
жсгкЕу![]() ,
,
гЩвбжЊЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
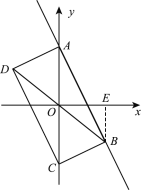
Ёп![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЌМДЕуBЕФзјБъЮЊЃЈ
ЃЌМДЕуBЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпОиаЮ![]() ЃЌ
ЃЌ
Ёр![]() = 4ЃЌ
= 4ЃЌ
Ёр![]() ЃЌ
ЃЌ
дкRtЁїOEBжа
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .
.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПгаетбљвЛИіЮЪЬт:ЬНОПКЏЪ§![]() ЕФЭМЯѓгыаджЪ.аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§
ЕФЭМЯѓгыаджЪ.аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОП.
ЕФЭМЯѓгыаджЪНјааСЫЬНОП.
ЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећ:
(1)КЏЪ§![]() ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ;
ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ;
(2)ЯТБэЪЧyгыxЕФМИзщЖдгІжЕ.
x | Ё | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | Ё |
y | Ё |
|
|
|
| 3 |
|
|
| m | Ё |
ЧѓmЕФжЕ;
(3)ШчЯТЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕу.ИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓ;

(4)НсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФвЛЬѕаджЪ: .