题目内容
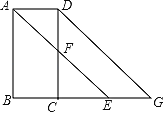
【题目】如图,一楼房AB后有一假山,其坡比i=1∶![]() ,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.
,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.

【答案】楼房AB的高为(35+10![]() )m.
)m.
【解析】
如下图,过点E作EF⊥AB于点F,EH⊥BC于点H,则∠FHC=90°,四边形BHEF是矩形,在Rt△FHC中由已知条件易得FH和CH的长,由BF=EH,EF=BH可得BF、EF的长,再在Rt△AEF中由已知条件求得AF的长即可由AB=AF+FB求得AB的长了.
如下图,过点E作EF⊥AB于点F,EH⊥BC于点H,
则∠FHC=90°,四边形BHEF是矩形,
∴EF=BH,BF=EH,∠AFE=90°,
∵斜坡CD的坡比:i=1∶![]() ,
,
∴tan∠ECH=![]() ,
,
∴∠ECH =30°,
∴EH=CE·sin30°=20×![]() =10(m),CH=CE·cos30°=20×
=10(m),CH=CE·cos30°=20×![]() =10
=10![]() (m).
(m).
又∵BC=25 m,
∴EF=BH=BC+CH=(25+10![]() )m,
)m,
∵在A点观测点E的俯角为45°,∠AFE=90°,
∴△AEF是等腰直角三角形,
∴AF=EF=(25+10![]() ) m.
) m.
又∵BF=EH=10 m,
∴AB=AF+BF=(35+10![]() ) m.
) m.
答:楼房AB的高为(35+10![]() )m.
)m.


练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目