题目内容
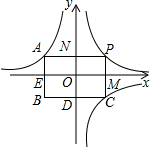 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
分析:易知四边形ABCP、四边形ODBE都是矩形,欲求四边形ODBE的面积,必须求出OE、OD的值,即CM、AN的值;设出点P的坐标,然后表示出A、C的坐标,即可得解.
解答:解:设P(a,b),则ab=k1;(a>0,b>0)
由于PC⊥x轴,所以P、C横坐标相同,将x=a代入y=
中,得:y=
;
即CM=OD=-
,同理可得:AN=OE=-
;
∴S矩形ODBE=OD•OE=
=
.
由于PC⊥x轴,所以P、C横坐标相同,将x=a代入y=
| k2 |
| x |
| k2 |
| a |
即CM=OD=-
| k2 |
| a |
| k2 |
| b |
∴S矩形ODBE=OD•OE=
| k22 |
| ab |
| k22 |
| k1 |
点评:此题主要考查了反比例函数图象上点的坐标意义,以及矩形面积的求法,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
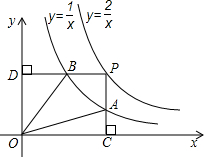 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
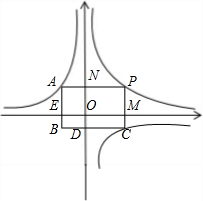 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
 (2012•德州)如图,两个反比例函数
(2012•德州)如图,两个反比例函数 如图,两个反比例函数y=
如图,两个反比例函数y=