题目内容
 (2012•德州)如图,两个反比例函数y=
(2012•德州)如图,两个反比例函数y=| 1 |
| x |
| 2 |
| x |
分析:设P的坐标是(a,
),推出A的坐标和B的坐标,求出∠APB=90°,求出PA、PB的值,根据三角形的面积公式求出即可.
| 1 |
| a |
解答:解:∵点P在y=
上,
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a,
)(a为正数),
∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=-
上,
∴A的坐标是(a,-
),
∵PB⊥y轴,
∴B的纵坐标是
,
∵B在y=-
上,
∴代入得:
=-
,
解得:x=-2a,
∴B的坐标是(-2a,
),
∴PA=|
-(-
)|=
,PB=|a-(-2a)|=3a,
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是:
PA×PB=
×
×3a=
.
故选C.
| 1 |
| x |
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a,
| 1 |
| a |
∵PA⊥x轴,
∴A的横坐标是a,
∵A在y=-
| 2 |
| x |
∴A的坐标是(a,-
| 2 |
| a |
∵PB⊥y轴,
∴B的纵坐标是
| 1 |
| a |
∵B在y=-
| 2 |
| x |
∴代入得:
| 1 |
| a |
| 2 |
| x |
解得:x=-2a,
∴B的坐标是(-2a,
| 1 |
| a |
∴PA=|
| 1 |
| a |
| 2 |
| a |
| 3 |
| a |
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| a |
| 9 |
| 2 |
故选C.
点评:本题考查了反比例函数和三角形面积公式的应用,关键是能根据P点的坐标得出A、B的坐标,本题具有一定的代表性,是一道比较好的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

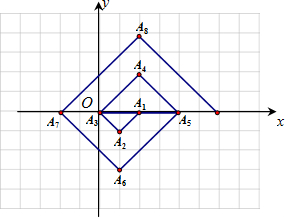 (2012•德州)如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为
(2012•德州)如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为 (2012•德州)如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
(2012•德州)如图给定的是纸盒的外表面,下面能由它折叠而成的是( ) (2012•德州)如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于
(2012•德州)如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于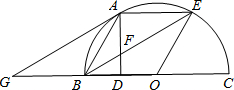 (2012•德州)如图,点A,E是半圆周上的三等分点,直径BC=2,AD⊥BC,垂足为D,连接BE交AD于F,过A作AG∥BE交BC于G.
(2012•德州)如图,点A,E是半圆周上的三等分点,直径BC=2,AD⊥BC,垂足为D,连接BE交AD于F,过A作AG∥BE交BC于G.