题目内容
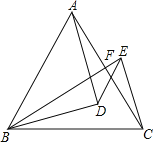
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
【答案】3.
【解析】
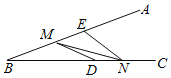
如图,作点D关于BA的对称点G,作点E关于BC的对称点H,连接GH交AB有M,交BC有N,连接DM、EN,此时DM+MN+NE的值最小.再证明∠HBG=90°,利用勾股定理即可解决问题.
如图所示:

作点D关于AB的对称点G,作点E关于BC的对称点H,
连接GH交AB于点M、交BC于点N,
连接DM、EN,
此时DM+MN+NE的值最小.
根据对称的性质可知:
DB=BG=3,∠GBE=∠DBE=20°,
BH=BE=3,∠HBD=∠EBD=20°,
∴∠GBH=60°,
∴△BGH是等边三角形,
∴GH=GB=HB=3,
∴DM+MN+NE的最小值为3.
故答案为3.

练习册系列答案
相关题目