Question

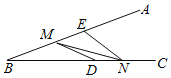
【题目】如图，△ABC为等腰直角三角形，△ABD为等边三角形，连接CD

（1）求∠ACD的度数

（2）作∠BAC的角平分线交CD于点E，求证：DE＝AE+CE

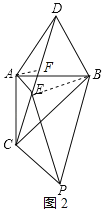
（3）在（2）的条件下，P为图形外一点，满足∠CPB＝60°，求证：EP平分∠CPB．

Answer 1

【答案】（1）15°；（2）见解析；（3）见解析

【解析】

（1）由等腰直角三角形和等边三角形的性质可得，，从而可得，再根据等腰三角形的性质和三角形内角和定理即可得；

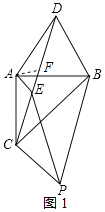
（2）如图1（见解析），在ED上截取，连接AF，可证是等边三角形，得出，再证明，由三角形全等的性质可得，即可得证；

（3）如图2（见解析），连接BE，证明，得出，，从而可求出，得出，证出B、E、C、P四点共圆，由圆周角定理得出，即可得证.

（1）为等腰直角三角形，为等边三角形

；

（2）如图1，在ED上截取，连接AF

，AE平分

是等边三角形，

在和中，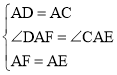

；

（3）如图2，连接BE

在和中，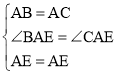

∴B、E、C、P四点共圆

（圆周角定理）

平分.