题目内容
19. 如图,直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为( )
如图,直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为( )| A. | 15° | B. | 25° | C. | 35° | D. | 55° |
分析 首先过点C作CE∥a,可得CE∥a∥b,然后根据两直线平行,内错角相等,即可求得答案.
解答  解:过点C作CE∥a,
解:过点C作CE∥a,
∵a∥b,
∴CE∥a∥b,
∴∠BCE=∠α,∠ACE=∠β=55°,
∵∠C=90°,
∴∠α=∠BCE=∠ABC-∠ACE=35°.
故选C.
点评 此题考查了平行线的性质.此题比较简单,注意掌握辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
| A. | a>1 | B. | a≤2 | C. | 1<a≤2 | D. | 1≤a≤2 |
14. 如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
 如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )
如图,AB为⊙O直径,已知∠DCB=20°,则∠DBA为( )| A. | 50° | B. | 20° | C. | 60° | D. | 70° |
4.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是( )


| A. | 222 | B. | 280 | C. | 286 | D. | 292 |
11.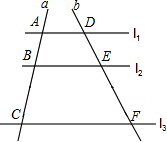 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )| A. | $\frac{8}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 10 |
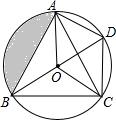 如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.


