题目内容
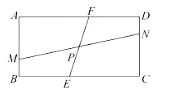
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() ,
,![]() 上,点
上,点![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,
,![]() 交于点
交于点![]() ,记
,记![]() .
.
(1)若![]() 的值是1,当
的值是1,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() 的值是
的值是![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
(3)若![]() 的值是3,当点
的值是3,当点![]() 是矩形的顶点,
是矩形的顶点,![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)作EH⊥BC于H,MQ⊥CD于Q,设EF交MN于点O.证明△FHE≌△MQN(ASA),即可解决问题.
(2)由题意:2a≤MN≤![]() a,a≤EF≤
a,a≤EF≤![]() a,当MN的长取最大时,EF取最短,此时k的值最大,最大值=
a,当MN的长取最大时,EF取最短,此时k的值最大,最大值=![]() ,当MN的最短时,EF的值取最大,此时k的值最小,最小值为
,当MN的最短时,EF的值取最大,此时k的值最小,最小值为![]() .
.
(3)连接FN,ME.由k=3,MP=EF=3PE,推出![]() ,推出
,推出![]() ,由△PNF∽△PME,推出
,由△PNF∽△PME,推出![]() =2,ME∥NF,设PE=2m,则PF=4m,MP=6m,NP=12m,接下来分两种情形①如图2中,当点N与点D重合时,点M恰好与B重合.②如图3中,当点N与C重合,分别求解即可.
=2,ME∥NF,设PE=2m,则PF=4m,MP=6m,NP=12m,接下来分两种情形①如图2中,当点N与点D重合时,点M恰好与B重合.②如图3中,当点N与C重合,分别求解即可.
(1)作![]() ,
,![]() ,如图1.
,如图1.
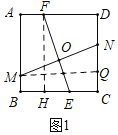
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
(2)∵![]() ,∴
,∴![]() .
.
由题意得,![]() ,
,![]() ,
,
当![]() 取最长时,
取最长时,![]() 可取到最短,此时
可取到最短,此时![]() 的值最大,最大值为
的值最大,最大值为![]() ,
,
当![]() 取最短时,
取最短时,![]() 可取到最长,此时
可取到最长,此时![]() 的值最小,最小值为
的值最小,最小值为![]() .
.
(3)连结![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
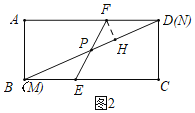
①当点![]() 与点
与点![]() 重合时, 如图2,点
重合时, 如图2,点![]() 恰好与点
恰好与点![]() 重合,过点
重合,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
②当点![]() 与点
与点![]() 重合时,如图3,过点
重合时,如图3,过点![]() 作
作![]() 于点
于点![]() ,
,

则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
综上所述,![]() 的值为
的值为![]() 或
或![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目