题目内容
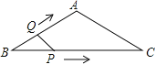
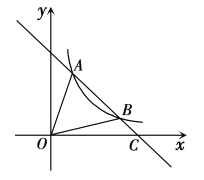
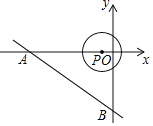
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上一动点,以点
轴上一动点,以点![]() 为圆心,以1个单位长度为半径作
为圆心,以1个单位长度为半径作![]() ,当
,当![]() 与直线
与直线![]() 相切时,点
相切时,点![]() 的坐标是_____.
的坐标是_____.
【答案】(﹣![]() ,0)或P(﹣
,0)或P(﹣![]() ,0)
,0)
【解析】
根据函数解析式求得![]() ,
,![]() ,得到
,得到![]() ,
,![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,设
,设![]() 与直线
与直线![]() 相切于
相切于![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
∵直线y=﹣![]() x﹣3交x轴于点A,交y轴于点B,
x﹣3交x轴于点A,交y轴于点B,
∴令x=0,得y=﹣3,令y=0,得x=﹣4,
∴A(﹣4,0),B(0.﹣3),
∴OA=4,OB=3,
∴AB=5,
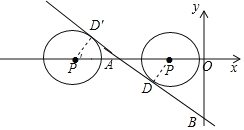
设⊙P与直线AB相切于D,
如图所示:连接PD,
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AP=![]() ,
,
∴OP=![]() 或OP=
或OP=![]() ,
,
∴P(﹣![]() ,0)或P(﹣
,0)或P(﹣![]() ,0).
,0).
故答案是:(﹣![]() ,0)或P(﹣
,0)或P(﹣![]() ,0).
,0).

练习册系列答案
相关题目