题目内容
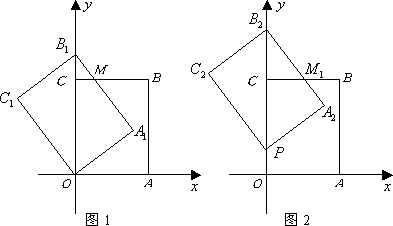
如图，若正△A1B1C1内接于正△ABC的内切圆，则
的值为
- A.
- B.
- C.
- D.
A
分析：由于△ABC、△A1B1C1都是正三角形，因此它们的外心与内心重合；可过O分别作AB、A1B1的垂线，连接OA、OA1；在构建的含特殊角的直角三角形中，用⊙O的半径分别表示出AB、A1B1的长，进而可求出它们的比例关系．
解答：
解：∵△A1B1C1和△ABC都是正三角形，∴它们的内心与外心重合；
如图：设圆的半径为R；
Rt△OAD中，∠OAD=30°，OD=R；
AD=OD•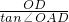
=
R，即AB=2R；
同理可求得A1B1=R；
∴=
=．
故选A．
点评：本题主要考查了等边三角形的性质：等边三角形的内心、外心、重心、垂心、旁心重合，称为等边三角形的中心（五心合一）．
分析：由于△ABC、△A1B1C1都是正三角形，因此它们的外心与内心重合；可过O分别作AB、A1B1的垂线，连接OA、OA1；在构建的含特殊角的直角三角形中，用⊙O的半径分别表示出AB、A1B1的长，进而可求出它们的比例关系．
解答：
解：∵△A1B1C1和△ABC都是正三角形，∴它们的内心与外心重合；如图：设圆的半径为R；
Rt△OAD中，∠OAD=30°，OD=R；
AD=OD•
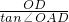=R，即AB=2R；同理可求得A1B1=
R；∴
==．故选A．
点评：本题主要考查了等边三角形的性质：等边三角形的内心、外心、重心、垂心、旁心重合，称为等边三角形的中心（五心合一）．
练习册系列答案
相关题目
