Question

如图（1），△ABC是正三角形，曲线DA₁B₁C₁…叫做“正三角形ABC的渐开线”，其中

A1C

，

A1B1，

B1C1

，…依次连接，它们的圆心依次按A，B，C循环．则曲线CA₁B₁C₁叫做正△ABC的1重渐开线，曲线CA₁B₁C₁A₂B₂C₂叫做正△ABC的2重渐开线，…，曲线CA₁B₁C₁A₂…A_nB_nC_n叫做正△ABC的n重渐开线．如图（2），四边形ABCD是正方形，曲线CA₁B₁C₁D₁…叫做“正方形ABCD的渐开线”，其中

A1D

，

A1B1

，

B1C1

，

C1D1

…依次连接，它们的圆心依次按A，B，C，D循环．则曲线DA₁B₁C₁D₁叫做正方形ABCD的1重渐开线，…，曲线DA₁B₁C₁D₁A₂…A_nB_nC_nD_n叫做正方形ABCD的n重渐开线．依次下去，可得正n形的n重渐开线（n≥3）．
若AB=1，则正方形的2重渐开线的长为18π；若正n边形的边长为1，则该正n边形的n重渐开线的长为

 

．

Answer 1

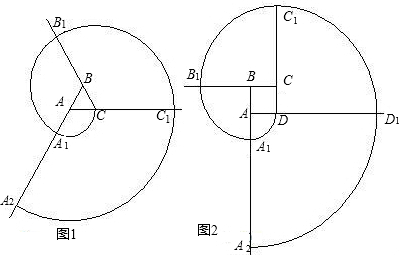
分析：利用n边形的外角与n的关系，然后再利用渐开线中第n重的关系求值．

解答：解：若正n边形的边长为1，
则该正n边形的第一重渐开线长=

90π×1

180

，二重=

90π×1

180

+

90π×2

180

，
第n重渐开线的长

90π×1

180

+

90π×2

180

+…+

90π×n

180

，
这是四边形，如果是n边形，
则内角和是（n-2）×180÷n，
所以正n边形的边长为1，
则该正n边形的n重渐开线的长为2π/n（1+2+…+n）+2π/n[（n+1）+（n+2）+…+（n+n）]+…+2π/n{[（n-1）n+1]+[（n-1）n+2]+…+[（n-1）n+n]=n（n²+1）π．

点评：本题的关键是明白n边形的外角与n的关系，然后再利用渐开线中第n重的关系求值．