Question

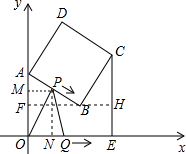
（2013•常熟市模拟）如图，正方形ABCD中，点A、B的坐标分别为（0，10）（8，4），点C在第一象限，且CE⊥x轴于E点，动点P在正方形ABCD的边上，从A出发沿A-B-C-D以每秒1个单位的速度作匀速运动，同时点Q（1，0）以相同的速度在x轴上沿正方向运动，当P点到达D点时，两点同时停止，设运动时间为t秒．
（1）当点Q运动至（20.5，0）时，则动点P在

BC

边上；
（2）求正方形点C坐标；
（3）问是否存在t（0≤t≤10）值，使△OPQ的面积最大？若存在，求出t值；若不存在，说明理由．

Answer 1

分析：（1）根据题意，得出正方形的边长，结合P，Q点的速度，分析可得答案；
（2）在Rt△AFB中，过点C作CE⊥x轴于点E，与FB的延长线交于点H，易得△ABF≌△BCH，进而可得C得坐标；
（3）过点P作PM⊥y轴于点M，PN⊥x轴于点N，易得△APM∽△ABF，根据相似三角形的性质，有

AP

AB

=

AM

AF

=

MP

BF

，设△OPQ的面积为S，计算可得答案．

解答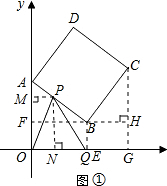：解：（1）过点B作BF⊥y轴于点F，
根据题意，AF=10-4=6，BF=8，
∴AB=

82+62

=10，
∴当点Q运动至（20.5，0）时，运动时间为：20.5-1=19.5（秒），
∴动点P在BC边上；

（2）过点C作CE⊥x轴于点E，与FB的延长线交于点H．
∵∠ABC=90°=∠AFB=∠BHC
∴∠ABF+∠CBH=90°，∠ABF=∠BCH，∴∠FAB=∠CBH，
在△ABF和△BCH中

∠BFA=∠CHF ∠HBC=∠FAB AB=BC

，
∴△ABF≌△BCH（AAS）．
∴AF=BH=6，CH=BF=8，
∴OE=FH=8+6=14，CE=8+4=12．
∴所求C点的坐标为（14，12）．

（3）过点P作PM⊥y轴于点M，PN⊥x轴于点N，
则△APM∽△ABF．
∴

AP

AB

=

AM

AF

=

MP

BF

．
∴

t

10

=

AM

6

=

MP

8

．
∴AM=

3

5

t，PM=

4

5

t．
∴PN=OM=10-

3

5

t，ON=PM=

4

5

t．
∵开始时Q（1，0），动点Q以相同速度在x轴正半轴上运动，
∴OQ=1+t，
设△OPQ的面积为S（平方单位）
∴S=

1

2

×（10-

3

5

t）（1+t）=5+

47

10

t-

3

10

t2（0≤t≤10）
∵a=-

3

10

＜0
∴当t=

- 47 10

2×(- 3 10 )

=

47

6

时，△OPQ的面积最大．
故答案为：BC．

点评：此题主要考查了相似形与函数的综合应用，要熟练掌握相似的性质和正方形的性质，并能够将他们与二次函数的应用有效的结合起来；解决此类问题，注意数形结合得思想的运用．