题目内容
 如图,在五边形ABCDE中,∠A+∠B+∠E=400°,∠BCD、∠CDE的平分线在五边形内相交于点O,∠1与∠2有怎样的数量关系?为什么?
如图,在五边形ABCDE中,∠A+∠B+∠E=400°,∠BCD、∠CDE的平分线在五边形内相交于点O,∠1与∠2有怎样的数量关系?为什么?考点:多边形内角与外角,三角形内角和定理
专题:
分析:根据五边形的内角和等于540°,由∠A+∠B+∠E=400°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠1与∠2之间的数量关系.
解答:解:∵五边形的内角和等于540°,∠A+∠B+∠E=400°,
∴∠BCD+∠CDE=540°-400°=140°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠1+∠2=
(∠BCD+∠CDE)=70°.
∴∠BCD+∠CDE=540°-400°=140°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠1+∠2=
| 1 |
| 2 |
点评:本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.

练习册系列答案
相关题目
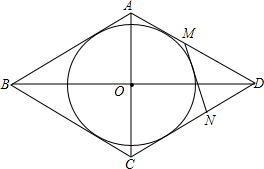 如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.
如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值. 如图所示,正方形ABCD中,M是AD的中点,点N在DC上,且DN=
如图所示,正方形ABCD中,M是AD的中点,点N在DC上,且DN=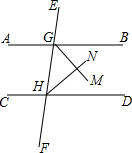 如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD.
如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD. 如图,AB∥CD,∠1=115°,∠2=140°.求∠3的度数.
如图,AB∥CD,∠1=115°,∠2=140°.求∠3的度数. 如图,已知点D为线段AC的中点,点B为线段DC的中点,DB=2,则线段AC=
如图,已知点D为线段AC的中点,点B为线段DC的中点,DB=2,则线段AC=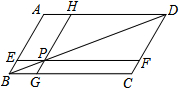 如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中哪两个平行四边形面积相等?为什么?
如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中哪两个平行四边形面积相等?为什么? 已知,如图,点E是BC延长线上一点,AE交CD于点F,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
已知,如图,点E是BC延长线上一点,AE交CD于点F,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE. 为了进一步了解某校九年级学生的身体素质,体育老师从该年级各班中随机抽取50名学生进行1分钟跳绳次数测试,以测试数据为样本,绘制出如图表.
为了进一步了解某校九年级学生的身体素质,体育老师从该年级各班中随机抽取50名学生进行1分钟跳绳次数测试,以测试数据为样本,绘制出如图表.