��Ŀ����
1��С������װ����������������ͼ1�������ε�ש���õ�ש������Գ�ͼ��Ҳ�����ĶԳ�ͼ�Σ�����Ч����ͼ2��ʾ��������ͼ1���֣�ש�����ĸ�С�����εı߳�����4cm��AB=JN=2cm���м�Ķ����CDEFGHIK�����˱��Σ���1����MA�ij��ȣ�
��2�������˱���CDEFGHIK�������
��3����֪С���ҳ����ĵ����DZ߳�Ϊ3.14�������Σ��øõ�ש������Ϻ�����γɶ��ٸ����˱��Σ�����ש���϶�Ŀ��Ⱥ��Բ��ƣ�

���� ��1������BK��NC�����ߵĽ���ΪO�����������ε����ʺ��ɶ������ON����������𰸣�
��2���������ߵó������κ�ֱ�������Σ��ֱ���������κ�ֱ�������ε���������ɵó��𰸣�
��3����������ε�ש�ı߳������������������С���ҳ����ĵ������������ɵó��𰸣�
��� �⣺��1������BK��NC�����ߵĽ���ΪO��
���ı���BCKN�������Σ�
���NOB=90�㣬OB=ON��
��BN=4cm��
���ɹ��ɶ����ã�BO=ON=2$\sqrt{2}$cm��
��JN=2cm��
��AM=JO=��2+2$\sqrt{2}$��cm��
��2����ͼ����С�����εĶԽ��ߣ����������ORZQ��
�������εı߳�Ϊ��2$\sqrt{2}$+4+2$\sqrt{2}$��cm����Ϊ��4$\sqrt{2}$+4��cm��
�������˱���CDEFGHIK�����ΪS������OQZR-4S��BOC=��4$\sqrt{2}$+4��2-4��$\frac{1}{2}$��2$\sqrt{2}$��2$\sqrt{2}$=��32+32$\sqrt{2}$��cm2��
��3�������ε�ש�ı߳�Ϊ��2����2+2$\sqrt{2}$��cm+��4$\sqrt{2}$+4��cm=��8+8$\sqrt{2}$��cm��
��3.14��=314cm��
��3142�£�8+8$\sqrt{2}$��2��263���飩��
���øõ�ש������Ϻ�����γ�263�����˱��Σ�
���� ���⿼����ƽ����Ƕ�����Ӧ�ã��ܹ�������ͼ���ǽ����Ĺؼ��������ѶȽϴ�ͬʱ�������������κ����˱��ε����ʼ����ɶ�����

| A�� | $\sqrt{5ab}$ | B�� | $\sqrt{4{a^2}}$ | C�� | $\sqrt{8a}$ | D�� | $\sqrt{\frac{a}{2}}$ |
| A�� | -9�� | B�� | -5�� | C�� | 5�� | D�� | 9�� |
| A�� | 10 | B�� | -6 | C�� | -6��10 | D�� | -10 |
 ��ͼ��һ�������ڵ�һ�����ڼ�x�ᡢy�����˶����ڵ�һ����������ԭ���˶�����1��0�������������Ű�ͼʾ��x�ᡢy��ƽ�еķ����������˶�����ÿ�����ƶ�һ�����ȵ�λ����ô��2015���Ӻ��������������λ�ã����꣩�ǣ�44��9����
��ͼ��һ�������ڵ�һ�����ڼ�x�ᡢy�����˶����ڵ�һ����������ԭ���˶�����1��0�������������Ű�ͼʾ��x�ᡢy��ƽ�еķ����������˶�����ÿ�����ƶ�һ�����ȵ�λ����ô��2015���Ӻ��������������λ�ã����꣩�ǣ�44��9����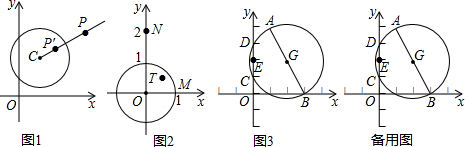
 ��ͼ��ʾ��OC�ǡ�AOD��ƽ���ߣ�OE�ǡ�BOD��ƽ���ߣ�
��ͼ��ʾ��OC�ǡ�AOD��ƽ���ߣ�OE�ǡ�BOD��ƽ���ߣ�