题目内容
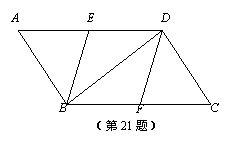
如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
 |
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,AB=CD.
∵点E、F分别是AD、BC的中点,
∴AE= AD,FC=
AD,FC= BC.
BC.
∴AE=CF.
在△AEB与△CFD中

∴△AEB≌△CFD.
(2)解:∵四边形EBFD是菱形,
∴BE=DE.
∴∠EBD=∠EDB.
∵AE=DE,
∴BE=AE.
∴∠A=∠ABE.
∵∠EBD+∠EDB+∠A+∠ABE=180°,
∴∠AB D=∠ABE+∠EBD=
D=∠ABE+∠EBD= ×180°=90°.
×180°=90°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若正比例函数y=2x与反比例 函数y=
函数y=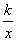 (k≠0)的图像相交,则当x<0时,交点位于( )
(k≠0)的图像相交,则当x<0时,交点位于( )
|
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |



 的图像,则两图像交点的横坐
的图像,则两图像交点的横坐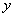 (km)与所用时间
(km)与所用时间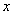 ( h)的函数关系图象;
( h)的函数关系图象;
 ,那么这个多边形的边数是 .
,那么这个多边形的边数是 .