题目内容
已知AD是BC边上的中线，如果BC=10cm，AC=4cm，AD=3cm，求△ABC的面积．考点：勾股定理的逆定理
专题：
分析：先根据AD是BC边上的中线BC=10cm得出CD=5cm，再由勾股定理的逆定理判断出△ACD是直角三角形，过点A作AE⊥BC于点E，根据三角形的面积公式求出AE的长，进而可得出结论．
解答：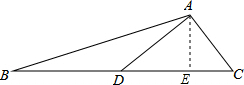
解：∵AD是BC边上的中线，BC=10cm，
∴CD=5cm．
∵32+42=52，即AD2+AC2=CD2，
∴△ACD是直角三角形．
过点A作AE⊥BC于点E，
∵AE=
=
=
，
∴S△ABC=
BC•AE=
×10×
=12cm2．
解：∵AD是BC边上的中线，BC=10cm，∴CD=5cm．
∵32+42=52，即AD2+AC2=CD2，
∴△ACD是直角三角形．
过点A作AE⊥BC于点E，
∵AE=
| AD•AC |
| CD |
| 3×4 |
| 5 |
| 12 |
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
点评：本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
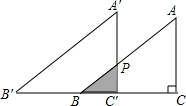如图所示，在Rt△ABC中，∠C=90°，BC=4cm，AC=3cm，若△A′B′C′与△ABC完全重合，令△ABC固定不动，将△A′B′C′沿CB所在的直线向左以1cm/s的速度移动．设移动xs后，△A′B′C′与△ABC的重合部分的面积为ycm2，求：