题目内容
 如图,已知△ABD∽△CBA.
如图,已知△ABD∽△CBA.
(1)若∠DAC=60°,∠C=36°,则∠BAD=________;
(2)此时是否有AB2=BD•BC?为什么?
(3)若AC=6,AD=3,AB=4,求CB的长.
解:(1)∵△ABD∽△CBA,
∴∠BAD=∠C,
∵∠C=36°,
∴∠BAD=36°,
故答案为:36°;
(2)有AB2=BD•BC,
理由是:∵△ABD∽△CBA,
∴ ,
,
∴AB2=BD•BC;
(3)∵△ABD∽△CBA
∴ ,
,
∴BD= =2,
=2,
而AB2=BD•BC,
∴BC= =8.
=8.
分析:(1)根据相似三角形性质得出∠BAD=∠C,代入求出即可;
(2)根据相似三角形的性质得出比例式,根据比例的性质推出即可;
(3)根据相似三角形的性质得出比例式,求出BD,再根据AB2=BD•BC,代入求出BC即可.
点评:本题考查了相似三角形的性质,注意:相似三角形的对应边成比例,即由△ABD∽△CBA可推出 =
=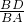 =
= .
.
∴∠BAD=∠C,
∵∠C=36°,
∴∠BAD=36°,
故答案为:36°;
(2)有AB2=BD•BC,
理由是:∵△ABD∽△CBA,
∴
 ,
,∴AB2=BD•BC;
(3)∵△ABD∽△CBA
∴
 ,
,∴BD=
 =2,
=2,而AB2=BD•BC,
∴BC=
 =8.
=8.分析:(1)根据相似三角形性质得出∠BAD=∠C,代入求出即可;
(2)根据相似三角形的性质得出比例式,根据比例的性质推出即可;
(3)根据相似三角形的性质得出比例式,求出BD,再根据AB2=BD•BC,代入求出BC即可.
点评:本题考查了相似三角形的性质,注意:相似三角形的对应边成比例,即由△ABD∽△CBA可推出
 =
=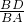 =
= .
. 
练习册系列答案
相关题目
 17、如图,已知∠ABD=∠BDA=∠ADC=∠DCA=75度.请你写出由已知条件能够推出的四个有关线段关系的正确结论(注意:不添加任何字母和辅助线,线段关系仅限于垂直、相等)
17、如图,已知∠ABD=∠BDA=∠ADC=∠DCA=75度.请你写出由已知条件能够推出的四个有关线段关系的正确结论(注意:不添加任何字母和辅助线,线段关系仅限于垂直、相等) (2012•江门模拟)如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.
(2012•江门模拟)如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F. 如图,已知△ABD沿BD平移到了△FCE的位置,BE=10,CD=4,则平移的距离是
如图,已知△ABD沿BD平移到了△FCE的位置,BE=10,CD=4,则平移的距离是 如图,已知∠ABD=∠ACD=90°,∠CBD=∠BCD,求证:AD平分∠BAC.
如图,已知∠ABD=∠ACD=90°,∠CBD=∠BCD,求证:AD平分∠BAC. 如图,已知△ABD和△ACE,AD=AE,∠1=∠2,要判定△ABD≌△ACE,还需要添加一个条件,这个条件可以是
如图,已知△ABD和△ACE,AD=AE,∠1=∠2,要判定△ABD≌△ACE,还需要添加一个条件,这个条件可以是