题目内容
如图，BC=
AB，M是AC的中点．若MB=4.5cm．求线段AB的长．
解：∵M是AC中点，
∴AM=MC=
AC，
∵BC=AB，
∴BC=
AC，AB=
AC，
则MB=MC-BC=AC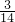-AC=
AC，
∵MB=4.5cm，
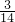∴AC=4.5cm，
∴AC=21cm，
∴AB=AM+MB=15cm．
分析：先根据M是线段AC的中点，AM=MC=AC，根据BC=AB，可用AC表示出BC、AB的长，由MB=MC-BC即可得出结论．
点评：本题主要考查了利用中点性质转化线段之间的倍分关系，灵活运用线段的和、差、倍、分转化线段之间的数量关系，难度适中．
∴AM=MC=
AC，∵BC=
AB，∴BC=
AC，AB=AC，则MB=MC-BC=
AC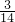-AC=AC，∵MB=4.5cm，
∴
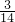AC=4.5cm，∴AC=21cm，
∴AB=AM+MB=15cm．
分析：先根据M是线段AC的中点，AM=MC=
AC，根据BC=AB，可用AC表示出BC、AB的长，由MB=MC-BC即可得出结论．点评：本题主要考查了利用中点性质转化线段之间的倍分关系，灵活运用线段的和、差、倍、分转化线段之间的数量关系，难度适中．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
13、如图，BC⊥AB，则图中阴影部分的面积为
如图，BC⊥AB，C为垂足，BC=8cm，AC=6cm，AB=10cm，则点B到AC的距离是
如图，BC⊥AB，CB=6cm，AB=8cm，AC=10cm，那么点B到AC的距离是如图，BC=
AB，D为AC的中点，
，则AB的长是( )
| A．3cm | B．4cm | C．5cm | D．6cm |
