题目内容
8.已知二次函数y=$\frac{1}{2}$(x+1)2+4.(1)写出抛物线的开口方向、顶点坐标和对称轴.
(2)画出此函数的图象,并说出此函数图象与y=$\frac{1}{2}$x2的图象的关系.
分析 (1)抛物线解析式是顶点式,可根据顶点式的坐标特点求开口方向,顶点坐标及对称轴;
(2)画出此函数的图象,利用平移的方法得出y=$\frac{1}{2}$x2的图象.
解答 解:(1)抛物线的开口方向向上、顶点坐标为(-1,4),对称轴为x=-1.
(2)如图,
将二次函数y=$\frac{1}{2}$(x+1)2+4的图象向右平移1个单位,再向下平移4个单位可得到y=$\frac{1}{2}$x2的图象.
点评 此题考查二次函数的性质,根据抛物线的顶点式,可确定抛物线的开口方向,顶点坐标(对称轴),最大(最小)值,增减性等.

练习册系列答案
相关题目
19.下列说法中正确的是( )
| A. | $\sqrt{9}$等于±3 | |
| B. | 若点P(2,a)和点Q(b,-3)关于x轴对称,则a-b的值为1 | |
| C. | 函数$y=\frac{{\sqrt{x+1}}}{x}$的自变量的取值范围是x>-1且x≠0 | |
| D. | -8的立方根是2 |
16.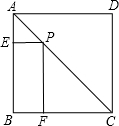 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 1 |
3.如果将二次函数y=3x2的图象向上平移5个单位,得到新的图象的二次函数表达式是( )
| A. | y=3x2-5 | B. | y=3(x-5)2 | C. | y=3x2+5 | D. | y=3(x+5)2-5 |
20.在直角三角形中,最大边的长度是最小边长度的2倍,那么最小内角的角度为( )
| A. | 15゜ | B. | 30゜ | C. | 45゜ | D. | 60゜ |