��Ŀ����
��ͼ1��ֱ��l1��y=2x��ֱ��l2��y=-3x+6�ཻ�ڵ�A��ֱ��l2��x�ύ�ڵ�B��ƽ����x���ֱ��y=n�ֱ�ֱ��l1��ֱ��l2��P��Q���㣨��P��Q����ࣩ
��1����A������Ϊ
��2����ͼ1������P���߶�AO�ϣ���x�����Ƿ����һ��H��ʹ�á�PQHΪ����ֱ�������Σ������ڣ������H�����ꣻ�������ڣ�˵�����ɣ�
��3����ͼ2�����Ե�PΪֱ�Ƕ��㣬����������ֱ�ǡ�PQF�����PQF���AOB�ص����ֵ����ΪS����S��n�ĺ�����ϵʽ����ע��n��ȡֵ��Χ��

��1����A������Ϊ
��
��
��
| 6 |
| 5 |
| 12 |
| 5 |
��
��
��
��| 6 |
| 5 |
| 12 |
| 5 |
��2����ͼ1������P���߶�AO�ϣ���x�����Ƿ����һ��H��ʹ�á�PQHΪ����ֱ�������Σ������ڣ������H�����ꣻ�������ڣ�˵�����ɣ�
��3����ͼ2�����Ե�PΪֱ�Ƕ��㣬����������ֱ�ǡ�PQF�����PQF���AOB�ص����ֵ����ΪS����S��n�ĺ�����ϵʽ����ע��n��ȡֵ��Χ��

��������1��������ֱ���ཻ�����ʣ�ʹ��ʽ��ȼ��ɵó��𰸣�
��2�����ȱ�ʾ��PQ�ij��ȣ������ó���PH=HQ�ҡ�PHQ=90��ʱ�Լ� ��PH=PQʱ��PQHΪ����ֱ�������Σ��ֱ�������ɣ�
��3���ֱ���ݵ�
��n��
ʱ�Լ���0��n��
ʱ��ʾ����PQF���AOB�ص����ֵ�������ɣ�
��2�����ȱ�ʾ��PQ�ij��ȣ������ó���PH=HQ�ҡ�PHQ=90��ʱ�Լ� ��PH=PQʱ��PQHΪ����ֱ�������Σ��ֱ�������ɣ�
��3���ֱ���ݵ�
| 6 |
| 11 |
| 6 |
| 5 |
| 18 |
| 11 |
��� �⣺��1����ֱ��l1��y=2x��ֱ��l2��y=-3x+6�ཻ�ڵ�A��
�⣺��1����ֱ��l1��y=2x��ֱ��l2��y=-3x+6�ཻ�ڵ�A��
��2x=-3x+6��
��ã�x=
��
��y=
��
���A��������
��
����
��2����y=n����n=2x��
��x=
n��
���P��
n��n����
n=-3x+6��
��x=2-
n��
���Q��2-
n��n����
��PQ=2-
n-
n=2-
n��
��PH��x����H����ͼ1�� ��PH=PQʱ��PQHΪ����ֱ�������Σ�
��2-
n=n��
n=
��
��
=
��
��H1��
��0����
��QH��x����H����ͼ������ͼ������QH=PQʱ��PQHΪ����ֱ�������Σ�
ͬ���ɵ�n=
2-
��
=
��
��H2��
��0����
��PH=HQ�ҡ�PHQ=90��ʱ����PQHΪ����ֱ��������HG��PQ���ɵ�PQ=2HG��
��2-
n=2n��n=
��
��
=
��2-
��
=
��
(
+
)=
��
��H3��
��0����
��H���������
��0������
��0������
��0����
��3����
��n��
ʱ��
��S=
PQ2=
(2-
n)2��
��0��n��
ʱ��2-
n-n=2-
n��
��S=
(2-
n+2-
n)•n=-
n2+2n��
 �⣺��1����ֱ��l1��y=2x��ֱ��l2��y=-3x+6�ཻ�ڵ�A��
�⣺��1����ֱ��l1��y=2x��ֱ��l2��y=-3x+6�ཻ�ڵ�A����2x=-3x+6��
��ã�x=
| 6 |
| 5 |
��y=
| 12 |
| 5 |
���A��������
| 6 |
| 5 |
| 12 |
| 5 |
��2����y=n����n=2x��
��x=
| 1 |
| 2 |
���P��
| 1 |
| 2 |
n=-3x+6��
��x=2-
| 1 |
| 3 |
���Q��2-
| 1 |
| 3 |
��PQ=2-
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
��PH��x����H����ͼ1�� ��PH=PQʱ��PQHΪ����ֱ�������Σ�
��2-
| 5 |
| 6 |
n=
| 12 |
| 11 |
| 1 |
| 2 |
| 12 |
| 11 |
| 6 |
| 11 |
��H1��
| 6 |
| 11 |
��QH��x����H����ͼ������ͼ������QH=PQʱ��PQHΪ����ֱ�������Σ�
ͬ���ɵ�n=
| 12 |
| 11 |
| 1 |
| 3 |
| 12 |
| 11 |
| 18 |
| 11 |
��H2��
| 18 |
| 11 |
��PH=HQ�ҡ�PHQ=90��ʱ����PQHΪ����ֱ��������HG��PQ���ɵ�PQ=2HG��
��2-
| 5 |
| 6 |
| 12 |
| 17 |
| 1 |
| 2 |
| 12 |
| 17 |
| 6 |
| 17 |
| 1 |
| 3 |
| 12 |
| 17 |
| 30 |
| 17 |
| 1 |
| 2 |
| 6 |
| 17 |
| 30 |
| 17 |
| 18 |
| 17 |
��H3��
| 18 |
| 17 |
��H���������
| 6 |
| 11 |
| 18 |
| 11 |
| 18 |
| 17 |
��3����
| 6 |
| 11 |
| 6 |
| 5 |
��S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
��0��n��
| 18 |
| 11 |
| 5 |
| 6 |
| 11 |
| 6 |
��S=
| 1 |
| 2 |
| 5 |
| 6 |
| 11 |
| 6 |
| 4 |
| 3 |
������������Ҫ������һ�κ������ۺ�Ӧ���Լ�����ֱ�������ε����ʣ��������ν�Ͻ��з��������ǽ���ؼ���ע�ⲻҪ©�⣮

��ϰ��ϵ�д�
 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
�����Ŀ
 ��ͼ����ֱ��l1��l2�Ľ������꣮��Ҫд���̣�
��ͼ����ֱ��l1��l2�Ľ������꣮��Ҫд���̣� 21����ͼ����ֱ��L1��L2��L3��L4������ƽ���ϵ�λ�ã�������һ��ֱ��Ϊ����ʽy+4=0��ͼ�Σ���˷���ʽͼ��Ϊ��������
21����ͼ����ֱ��L1��L2��L3��L4������ƽ���ϵ�λ�ã�������һ��ֱ��Ϊ����ʽy+4=0��ͼ�Σ���˷���ʽͼ��Ϊ��������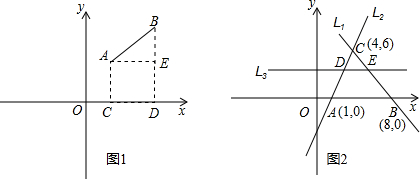
 ��2013•��������ͼ����ֱ��l1����AB�ķ���ƽ�Ƶõ�ֱ��l2������1=50�㣬���2�Ķ����ǣ�������
��2013•��������ͼ����ֱ��l1����AB�ķ���ƽ�Ƶõ�ֱ��l2������1=50�㣬���2�Ķ����ǣ�������