��Ŀ����
����Ŀ���ۺ���ʵ����
�����龳��������ת�е���ѧ
��֪�ھ���![]() �У�
��![]() ��
��![]() ���Ե�
���Ե�![]() Ϊ��ת���ģ���ʱ����ת����
Ϊ��ת���ģ���ʱ����ת����![]() ����ת��Ϊ
����ת��Ϊ![]() ���õ�����
���õ�����![]() ����
����![]() ����
����![]() ����
����![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ����
����![]() ����
����![]() ��
��
�������룺
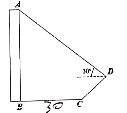
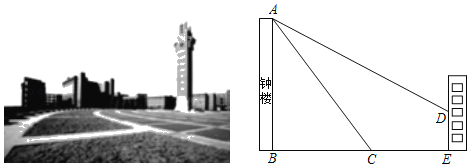
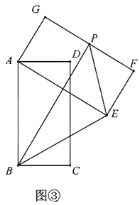
��1����ͼ�٣�����![]() ����
����![]() ����ʱ�����߶�
����ʱ�����߶�![]() �ij��ȣ�
�ij��ȣ�
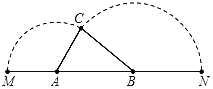
����̽����
��2����ͼ�ڣ�����![]() �����߶�
�����߶�![]() ��ʱ��
��ʱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() �����߶�
�����߶�![]() �ij��ȣ�
�ij��ȣ�
��3�����![]() ��
��![]() ��������ѡһ��������ѡ______�⣮
��������ѡһ��������ѡ______�⣮
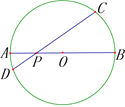
![]() �⣺��ͼ�ۣ����
�⣺��ͼ�ۣ����![]() Ϊ��
Ϊ��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��![]() ���ھ���
���ھ���![]() ��ת�����У�
��ת�����У�![]() ������Ƿ�������ֵ����������ֱ��д��������ֵ������������˵�����ɣ�
������Ƿ�������ֵ����������ֱ��д��������ֵ������������˵�����ɣ�
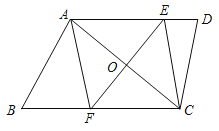
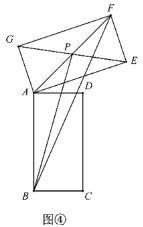
![]() �⣺��ͼ�ܣ����
�⣺��ͼ�ܣ����![]() Ϊ����
Ϊ����![]() �Խ��߽��㣬����
�Խ��߽��㣬����![]() ��
��![]() ���ھ���
���ھ���![]() ��ת�����У�
��ת�����У�![]() ������Ƿ�������ֵ����������ֱ��д��������ֵ������������˵�����ɣ�
������Ƿ�������ֵ����������ֱ��д��������ֵ������������˵�����ɣ�


���𰸡���1��CE= 2-![]() ����2��DH=
����2��DH=![]() ����3��A�⣺�������ֵ
����3��A�⣺�������ֵ![]() +1��B�⣺�������ֵ
+1��B�⣺�������ֵ![]() ��
��
��������
��1������ת�����ʿɵ�AE=AB�����ù��ɶ��������DE�ij������ɵ�CE�ij���
��2����ͼ������ת�����ʼ��������ʿɵ�AE=CD����AEF=��B=90�������ݵ�![]() �����߶�
�����߶�![]() �Ͽɵ�AE��CF������HL��֤����ACD�ա�CAE���ɵá�CAH=��ACH������֤��AH=CH����Rt��ADH�У����ù��ɶ����з������DH�ij����ɣ�
�Ͽɵ�AE��CF������HL��֤����ACD�ա�CAE���ɵá�CAH=��ACH������֤��AH=CH����Rt��ADH�У����ù��ɶ����з������DH�ij����ɣ�
��3��A�⣺��ͼ������PA����BM��PE����PE�ӳ�����M���ɵ�PΪFG�е�ɵ�PF=PG=1�����ù��ɶ����ɵ�PA=PE=![]() �����ɵó�S��BEP=
�����ɵó�S��BEP=![]() PE��BM=
PE��BM=![]() BM���ɵõ�BM���ʱ����BEP���������������ε����߹�ϵ��ֱ�������ε��������BM�����ֵ���ɵô𰸣�
BM���ɵõ�BM���ʱ����BEP���������������ε����߹�ϵ��ֱ�������ε��������BM�����ֵ���ɵô𰸣�
B�⣺��ͼ������B��BM��FA����FA�ӳ�����M�����ù��ɶ��������AF�ij������ݾ������ʿ����PF�ij����ɵó�S��BFP=![]() PF��BM���ɵ�BM���ʱ��BFP�����������������ε����߹�ϵ�ó�BM�����ֵ���ɵô𰸣�
PF��BM���ɵ�BM���ʱ��BFP�����������������ε����߹�ϵ�ó�BM�����ֵ���ɵô𰸣�
��1�����Ե�![]() Ϊ��ת���ģ���ʱ����ת����
Ϊ��ת���ģ���ʱ����ת����![]() ���õ�����
���õ�����![]() ��
��![]() ��
��![]() ��
��
��AE=AB=CD=2��AD=BC=1��
��DE=![]() =
=![]() ��
��
��CE=CD-DE=2-![]() ��
��
��2���Ե�![]() Ϊ��ת���ģ���ʱ����ת����
Ϊ��ת���ģ���ʱ����ת����![]() ���õ�����
���õ�����![]() ��
��![]() ��
��![]() ��
��
��AE=AB=CD=2����AEF
�ߵ�![]() �����߶�
�����߶�![]() �ϣ�
�ϣ�
���AEC=90����
��Rt��ACD��Rt��CAE��![]() ��
��
��Rt��ACD��Rt��CAE��
���CAH=��ACH��
��AH=CH��
��Rt��ADH��AH2=DH2+AD2��
�ࣨCD-DH��2=DH2+AD2������2-DH��2=DH2+12��
��ã�DH=![]() ��
��
��3��A�⣺
��ͼ������PA����BM��PE����PE�ӳ�����M��
�ߵ�PΪGF�е㣬
��PG=PF=1��
��PA=PE=![]() =
=![]() ��
��
��S��BEP=![]() PE��BM=
PE��BM=![]() BM��
BM��
�൱BM���ʱ����BEP��������
��BM��BP��BP��AB+AP=2+![]() ��
��
��BM��2+![]() ����BM�����ֵΪ2+
����BM�����ֵΪ2+![]() ��
��
���BEP����������ֵΪ��![]() BM=
BM=![]() ����2+
����2+![]() ��=
��=![]() +1��
+1��

B�⣺
��ͼ������B��BM��FA����FA�ӳ�����M��
��AB=2��BC=1������AEFG�ɾ���ABCD��ת���ã�
��AF=![]() =
=![]() ��
��
��PF=![]() AF=
AF=![]() ��
��
��S��BFP=![]() PF��BM=
PF��BM=![]() BM��
BM��
�൱BM���ʱ����BFP��������
��BM��AB��
��BM�����ֵΪAB=2��
���BFP����������ֵΪ![]() BM=
BM=![]() ��2=
��2=![]() ��
��


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�