题目内容
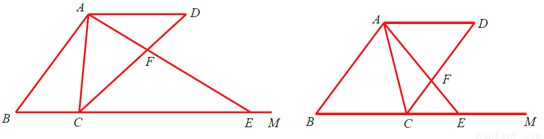
已知AB=5,AD=4,AD∥BM, 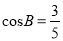 (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x, 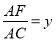 .
.
(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
题目内容
已知AB=5,AD=4,AD∥BM, 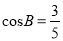 (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x, 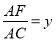 .
.
(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案