��Ŀ����
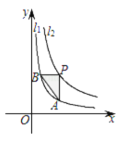
����Ŀ����ͼ1����һ���������͵��ݽ��棬����![]() �������ߵ�һ���֣��������߿������ҡ��Գ���������ˮƽ��
�������ߵ�һ���֣��������߿������ҡ��Գ���������ˮƽ��![]() ��
��![]() ��
��![]() ����ˮƽ��
����ˮƽ��![]() ��ֱ������֧����
��ֱ������֧����![]() �ף�
�ף�![]() �ף�
�ף�![]() ��.
��.
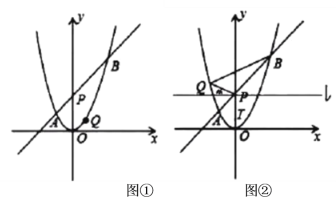
��1����ͼ1��Ϊ�˰�ȫ���ۣ������֧��![]() ��
��![]() ����ˮƽ��
����ˮƽ��![]() ������һ��
������һ��![]() ��Ϊ�����ϵ�֧�ŵ㣬�ù̶���������
��Ϊ�����ϵ�֧�ŵ㣬�ù̶���������![]() ��
��![]() �������������ͽ���֧�żӹ̣�������ʡʱ��
�������������ͽ���֧�żӹ̣�������ʡʱ��![]() ��
��![]() ֮��ľ�����_________.
֮��ľ�����_________.
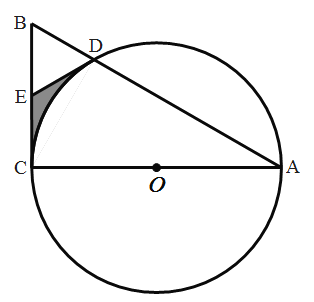
��2����ͼ2����ˮƽ��![]() ������һ��
������һ��![]() �׳�������
�׳�������![]() ��
��![]() ��
��![]() �Ҳࣩ���ù̶���������
�Ҳࣩ���ù̶���������![]() ��
��![]() �������������ͽ���֧�żӹ̣�������ʡʱ��
�������������ͽ���֧�żӹ̣�������ʡʱ��![]() ��
��![]() ֮��ľ�����_______________.
֮��ľ�����_______________.
���𰸡�![]()
![]()
��������
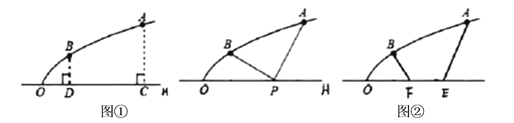
��1���Ե�OΪԭ�㣬OC����ֱ��Ϊy�ᣬ��ֱ��OC��ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ�����ô���ϵ����ȷ�����κ����Ľ���ʽ���ӳ�BD��MʹMD=BD������AM��OC�ڵ�P�����P��Ϊ�������ô���ϵ����ȷ��ֱ��M'A'�Ľ���ʽ���Ӷ���õ�P�������꣬�Ӷ����O��P֮��ľ��룻
��2������![]() ��
��![]() ƽ����
ƽ����![]() ����
����![]() ����
����![]() �����
�����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() �����
�����![]() ������.
������.
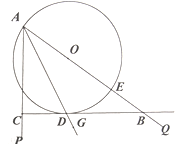
��1����ͼ����ƽ��ֱ������ϵ���Ե�![]() Ϊԭ�㣬
Ϊԭ�㣬![]() ����ֱ��Ϊ
����ֱ��Ϊ![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() ��ֱ��Ϊ
��ֱ��Ϊ![]() �ᣩ���ӳ�
�ᣩ���ӳ�![]() ��
��![]() ʹ
ʹ![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() �����
�����![]() ������.
������.

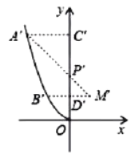
�������ߵĺ�������ʽΪ![]() ��
��
������֪��ת���![]() ������Ϊ
������Ϊ![]() .�������ʽ��
.�������ʽ��![]()
![]() �����ߵĺ�������ʽΪ��
�����ߵĺ�������ʽΪ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
![]()
![]() ��
��![]() ������Ϊ
������Ϊ![]()
����![]() ��
��![]() ���ֱ��
���ֱ��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
![]() ������ʡʱ����
������ʡʱ����![]() ��
��![]() ֮��ľ�����
֮��ľ�����![]() ��.
��.
��2������![]() ��
��![]() ƽ����
ƽ����![]() ����
����![]() ����
����![]() �����
�����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() �����
�����![]() ������.
������.
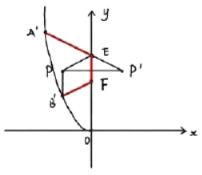
![]()
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
![]() ������Ϊ
������Ϊ![]()
����![]() ��
��![]() �����������ֱ��
�����������ֱ��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
![]() ������ʡʱ����
������ʡʱ����![]() ��
��![]() ֮��ľ�����
֮��ľ�����![]() ��.
��.

����Ŀ��Ϊ�����հ��꼶��ѧ���Ծ��������������Ѷ�ϵ�����������ʦ�����ѡȡһ��ˮƽ�൱�İ��꼶�༶����Ԥ�⣬�����Գɼ��ֲ�������д����������Ƴ�Ƶ���ֲ�������(�ɼ��÷־�Ϊ����)��
��� | �ɼ����� | Ƶ��Ƶ�� | Ƶ�� |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
�ϼ� | 40 | 1.00 |
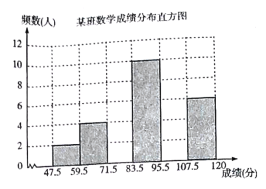
���ݱ����ṩ����Ϣ����������⣺
��1��Ƶ���ֲ����е�![]() ��
��![]() ��
��![]() ��
��
��2����֪ȫ�����꼶����200����(ƽ��ÿ��40��)��������Ծ���⣬108�ּ�����Ϊ���㣬Ԥ�����������ԼΪ ��72�ּ�����Ϊ����Ԥ�Ƽ��������ԼΪ ������İٷֱ�ԼΪ ��
��3����������Ƶ���ֲ�ֱ��ͼ.