��Ŀ����
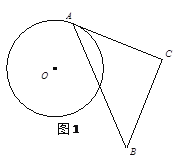
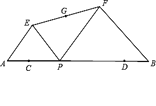
����Ŀ����ͼ����֪AB=12����C��D��AB�ϣ���AC=DB=2����P�ӵ�C���߶�CD���D�˶����˶�����Dֹͣ������AP��BPΪб����AB��ͬ�����Rt��APE�͵���Rt��PBF������EF��ȡEF���е�G������˵������ȷ���У� ��
�١�EFP�����Բ��Բ��Ϊ��G��
���ı���AEFB��������䣻
��EF���е�G�ƶ���·����Ϊ4��
A. 0�� B. 1�� C. 2�� D. 3��
���𰸡�C
��������
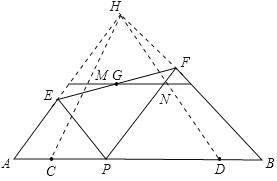
������ͼ���ֱ��ӳ�AE��BF���ڵ�H��
������Rt��APE�͵���Rt��PBF�����A=��FPB=45������B=��EPA=45������AH��PF��BH��PE����EPF=180�㩁��EPA����FPB=90�������ı���EPFHΪƽ���ı��Σ���EF��HP����ƽ�֣���GΪEF���е㣬��GҲΪPH�е㣬����P���˶������У�Gʼ��ΪPH���е㣬��G�����й켣Ϊ��HCD����λ��MN����CD=12��2��2=8����MN=4����G���ƶ�·����Ϊ4������EF���е�G�ƶ���·����Ϊ4����ȷ��
��GΪEF���е㣬��EPF=90������١�EFP�����Բ��Բ��Ϊ��G����ȷ����٢���ȷ��
����PG����PG��PF�����EFP�����Բ��AB�ཻ����������
����P�ӵ�C���߶�CD���D�˶����˶�����Dֹͣ������֤��EPF=90���������ı��������������ֱ�������ε�����ͣ���cp=x�����ı������S=![]() ����AP�����������ı��ε����SҲ����֮�仯����������
����AP�����������ı��ε����SҲ����֮�仯����������
��ѡB��

 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
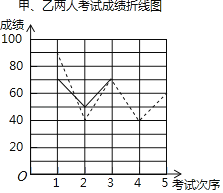
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�����Ŀ���ס�����λͬѧ5����ѧ�ɼ�ͳ����������ǵ�5���ܳɼ���ͬ��С���������ǵijɼ��������в�������ͳ��ͼ������ͬѧ������������⣮
���У�������ͼΪ���ߡ��ҵ�����ͼΪʵ�ߣ�
�ס������˵���ѧ�ɼ�ͳ�Ʊ�
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 | a | 70 |
��1��a���� ����![]() �� ����
�� ����
��2�������ͼ�б�ʾ�ҳɼ��仯��������ߣ�
��3��S2����260���ҳɼ��ķ������� �����ɿ����� ���ijɼ��Ƚ��ȶ�������������������������ƽ�����ͷ���ĽǶȷ������� ������ѡ�У�